题目内容
设集合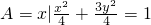 ,B={y|y=x2},则A∩B=
,B={y|y=x2},则A∩B=
- A.[-2,2]
- B.[0,2]
- C.[0,+∞)
- D.{(-1,1),(1,1)}
B
分析:先化简集合A和B,然后由交集的定义求得结果.
解答:∵集合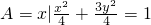 ={x|-2≤x≤2}
={x|-2≤x≤2}
B={y|y=x2}={x|x≥0}
∴A∩B={x|0≤x≤2}
故选:B.
点评:此题以圆锥曲线的性质为平台,考查集合的交集定义,属于中档题.
分析:先化简集合A和B,然后由交集的定义求得结果.
解答:∵集合
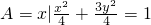 ={x|-2≤x≤2}
={x|-2≤x≤2}B={y|y=x2}={x|x≥0}
∴A∩B={x|0≤x≤2}
故选:B.
点评:此题以圆锥曲线的性质为平台,考查集合的交集定义,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 ,B={y|y=2x},则A∩B=( )
,B={y|y=2x},则A∩B=( ) ,B={y|y=x2},则A∩B=( )
,B={y|y=x2},则A∩B=( ) ,B={y|y=lg(x2+1)},则(CUA)∩B=( )
,B={y|y=lg(x2+1)},则(CUA)∩B=( ) ,B={y|y=2x},则A∩B=( )
,B={y|y=2x},则A∩B=( ) ,B={y|y=2x},则A∩B=( )
,B={y|y=2x},则A∩B=( )