题目内容
7．斜三棱柱一个侧面面积为5$\sqrt{3}$，这个侧面与所对棱的距离是2$\sqrt{3}$，此棱柱的体积为15．分析 将该斜三棱柱补成一个四棱柱，将其放倒使侧面与它所对的棱的距离为2$\sqrt{3}$，成为四棱柱的高，然后根据四棱柱的体积公式求体积．最后除以2得到三棱柱的体积．
解答 解：将该斜三棱柱补成一个四棱柱，该四棱柱的底面积为5$\sqrt{3}$，高为2$\sqrt{3}$，
故四棱柱的体积为5$\sqrt{3}$×2$\sqrt{3}$=30，
∴V斜三棱柱=$\frac{1}{2}×30$=15．
故答案为：15．
点评 本题考查棱柱的体积的计算方法，本题采用补图形的方法，这样可以降低运算量，本题考查学生空间想象能力，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
4．在△ABC中，已知cosA=$\frac{3}{5}$，cosB=$\frac{15}{17}$，则cosC等于（ ）
| A． | -$\frac{13}{85}$ | B． | $\frac{13}{85}$ | C． | -$\frac{77}{85}$ | D． | $\frac{77}{85}$ |
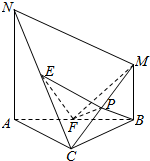已知△ABC，$AC=BC=\sqrt{2}a$，∠ACB=90°，过点A，B作线段AN，BM分别与△ABC所在的平面垂直，且AN=AB=2BM，E，F，P分别是线段NC，AB，MC的中点．