题目内容

1．棱长为a的正方体可任意摆放，则其在水平平面上投影面积的最大值为（　　）
A．$\sqrt{3}$a2B．$\sqrt{2}$a2C．$\frac{3\sqrt{3}}{4}$a2D．2a2

分析 确定正方体ABCD-A′B′C′D′投影面积最大时，是投影面α与平面AB′C平行，从而求出投影面积的最大值．

解答 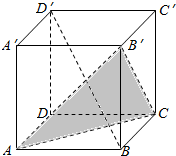解：设正方体为ABCD-A′B′C′D′投影最大时候，是投影面α与平面AB′C平行，
三个面的投影为三个全等的菱形，其对角线为$\sqrt{2}$a，
即投影面上三条对角线构成边长为$\sqrt{2}$a的等边三角形，如图所示；
∴投影的面积=2S△AB′C=2×$\frac{1}{2}$×$\sqrt{2}$a×$\frac{\sqrt{6}}{2}$a=$\sqrt{3}$a2．
故选：A．

点评 本题考查了平行投影及平行投影作图法，是计算投影面积的问题，解题时应注意投影图形的变化，是中档题目．

练习册系列答案
相关题目
11．已知函数g（x）=$\left\{\begin{array}{l}{{e}^{x}，x＞1}\\{\sqrt{{1-x}^{2}}，-1≤x≤1}\end{array}\right.$则${∫}_{-1}^{2}$g（x）dx=$\frac{π}{2}$+e2-e．
12．如图，在四棱锥S-ABCD中，底面是边长为2的正方形，SA⊥底面ABCD，且SA=2，E为SC的中点，则直线BE与平面ABCD所成角的正弦值为$\frac{\sqrt{3}}{3}$．
9．设a为非零实数，偶函数f（x）=x2+a|x-m|+1，x∈R在区间（1，2）上只有一个零点，则实数a的取值范围为-$\frac{5}{2}$＜a＜-2．
16．如图，在四棱锥A-BCDE中，底面DEBC为矩形，侧面ABC⊥底面BCDE，BC=2，CD=$\sqrt{2}$，AB=AC．
（1）求证：BE⊥面ABC；
（2）设△ABC为等边三角形，求直线CE与平面ABE所成角的大小．
6．函数$f（x）=\left\{\begin{array}{l}{a}^{x}，x≥0\\（3-a）x+\frac{a}{2}，x＜0\end{array}\right.$为区间（-∞，+∞）上的单调增函数，则实数a的取值范围为（1，2]．
13．直线x+$\sqrt{3}$y-1=0的斜率为（　　）
A．$\frac{\sqrt{3}}{3}$B．$\sqrt{3}$C．-$\frac{\sqrt{3}}{3}$D．-$\sqrt{3}$
10．设集合M={x|x∈Z且-10≤x≤-3}，N={x|x∈Z且|x|≤5 }，则M∪N中元素的个数为（　　）
A．11B．10C．16D．15
11．在平面直角坐标系xOy中，已知∠α的顶点为原点O，其始边与x轴正方向重合，终边过两曲线y=$\sqrt{x+3}$和y=$\sqrt{1-x}$的交点，则cos2α+cot（$\frac{3π}{2}$+α）=-$\frac{1}{3}$+$\sqrt{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网