题目内容
在极坐标系中，已知圆C经过点P
，圆心为直线ρsin
＝－
与极轴的交点，求圆C的极坐标方程．
，圆心为直线ρsin＝－与极轴的交点，求圆C的极坐标方程．ρ＝2cosθ
圆C的圆心为直线ρsin＝－与极轴的交点，
∴在ρsin＝－中令θ＝0，得ρ＝1.
∴圆C的圆心坐标为(1，0)．
∵圆C经过点P，
∴圆C的半径为PC＝
＝1.
∴圆C经过极点．
∴圆C的极坐标方程为ρ＝2cosθ.
＝－与极轴的交点，∴在ρsin
＝－中令θ＝0，得ρ＝1.∴圆C的圆心坐标为(1，0)．
∵圆C经过点P
，∴圆C的半径为PC＝
＝1.∴圆C经过极点．
∴圆C的极坐标方程为ρ＝2cosθ.
练习册系列答案
名校课堂系列答案
相关题目
于A、B两点，则|AB|= ．
的极坐标方程为
，直线
的参数方程为
为参数），点
的极坐标为
，设直线
、
.
的值.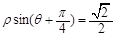 
，则极点到这条直线的距离是 ．
(t为参数)相交于A、B两点，求|AB|.
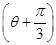，它们相交于A、B两点，求线段AB的长．
（
为参数且
）与曲线
（
是参数且
），则直线
与曲线
的交点坐标为 .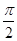
(ρ∈R)和ρcos θ＝2