题目内容
 如图,点P在以AB为直径的半圆上移动,且AB=1,过点P作圆的切线PC,使PC=1.连接BC,当点P在什么位置时,四边形ABCP的面积等于
如图,点P在以AB为直径的半圆上移动,且AB=1,过点P作圆的切线PC,使PC=1.连接BC,当点P在什么位置时,四边形ABCP的面积等于| 1 | 2 |
分析:设∠PAB=α,连接PB.根据题意设出PA和PB,利用PC是切线推断出∠BPC=α.利用三角形面积公式分别表示出S△APB和S△BPC,利用两角和公式和二倍角公式整理后,利用正弦函数的性质求得α.
解答: 解:设∠PAB=α,连接PB.
解:设∠PAB=α,连接PB.
∵AB是直径,∴∠APB=90°.
又AB=1,∴PA=cosα,PB=sinα.
∵PC是切线,∴∠BPC=α.又PC=1,
∴S四边形ABCP=S△APB+S△BPC
=
PA•PB+
PB•PC•sinα=
cosαsinα+
sin2α=
sin2α+
(1-cos2α)
=
(sin2α-cos2x)+
=
sin(2α-
)+
由已知,
sin(2α-
)+
=
∴sin(2α-
)=
又α?(0,
),
∴2α-
∈(-
,
).
∴2α-
=
,∴α=
故当点P位于AB的中垂线与半圆的交点时,
四边形ABCP的面积等于
 解:设∠PAB=α,连接PB.
解:设∠PAB=α,连接PB.∵AB是直径,∴∠APB=90°.
又AB=1,∴PA=cosα,PB=sinα.
∵PC是切线,∴∠BPC=α.又PC=1,
∴S四边形ABCP=S△APB+S△BPC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
=
| 1 |
| 4 |
| 1 |
| 4 |
| ||
| 4 |
| π |
| 4 |
| 1 |
| 4 |
| ||
| 4 |
| π |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
∴sin(2α-
| π |
| 4 |
| ||
| 2 |
| π |
| 2 |
∴2α-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴2α-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
四边形ABCP的面积等于
| 1 |
| 2 |
点评:本题主要考查了在实际问题中建立三角函数模型.注重了基础知识和基本运算能力的考查.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
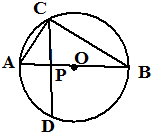 如图,点C在以AB为直径的⊙O上,CD⊥AB于点P,设AP=a,PB=B.
如图,点C在以AB为直径的⊙O上,CD⊥AB于点P,设AP=a,PB=B.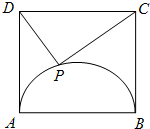 如图,ABCD是边长为4的正方形,动点P在以AB为直径的圆弧APB上,则
如图,ABCD是边长为4的正方形,动点P在以AB为直径的圆弧APB上,则 如图,点P在以AB为直径的半圆上移动,且AB=1,过点P作圆的切线PC,使PC=1.连接BC,当点P在什么位置时,四边形ABCP的面积等于
如图,点P在以AB为直径的半圆上移动,且AB=1,过点P作圆的切线PC,使PC=1.连接BC,当点P在什么位置时,四边形ABCP的面积等于 ?
? ?
?