题目内容
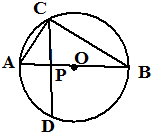 如图,点C在以AB为直径的⊙O上,CD⊥AB于点P,设AP=a,PB=B.
如图,点C在以AB为直径的⊙O上,CD⊥AB于点P,设AP=a,PB=B.(1)求弦CD的长;
(2)如果a+b=10,求ab的最大值,并求出此时a,b的值.
分析:(1)依题意,利用射影定理,PC2=AP•PB即可求得弦CD的长;
(2)利用基本不等式ab≤(
)2当且仅当“a=b”时“=”成立,即可求得答案.
(2)利用基本不等式ab≤(
| a+b |
| 2 |
解答:解:(1)∵AB为⊙O的直径,CD⊥AB于点P,
∴在直角三角形ACB中,由射影定理知,PC2=AP•PB,
∵AP=a,PB=b,
∴CD=2PC=2
=2
,
(2)∵a+b=10,
∴ab≤(
)2=25,当且仅当“a=b=5”时“=”成立.
∴在直角三角形ACB中,由射影定理知,PC2=AP•PB,
∵AP=a,PB=b,
∴CD=2PC=2
| PC2 |
| ab |
(2)∵a+b=10,
∴ab≤(
| a+b |
| 2 |
点评:本题考查与圆有关的线段,突出考查射影定理与基本不等式的应用,属于中档题.

练习册系列答案
相关题目
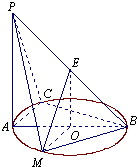 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,,点E为线段PB的中点,点M在AB弧上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,,点E为线段PB的中点,点M在AB弧上,且OM∥AC.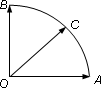
 已知|→|=|→|=1,它们的夹角为600,如图:点C在以O为圆心的圆
已知|→|=|→|=1,它们的夹角为600,如图:点C在以O为圆心的圆 已知|→|=|→|=1,它们的夹角为600,如图:点C在以O为圆心的圆
已知|→|=|→|=1,它们的夹角为600,如图:点C在以O为圆心的圆