题目内容
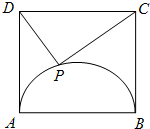如图，ABCD是边长为4的正方形，动点P在以AB为直径的圆弧APB上，则| PC |
| PD |
[0，16]
[0，16]
．分析：以AB中点为坐标原点，AB所在直线为x轴建立如图坐标系，可得C（2，4），D（-2，4），P（2cosα，2sinα），得到
、
坐标，用向量数量积的坐标公式化简，得
•
=16-16sinα，再结合α∈[0，π]，不难得到
•
的取值范围．
| PC |
| PD |
| PC |
| PD |
| PC |
| PD |
解答：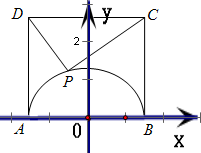
解：以AB中点为坐标原点，AB所在直线为x轴建立如图坐标系
则圆弧APB方程为x2+y2=4，（y≥0），C（2，4），D（-2，4）
因此设P（2cosα，2sinα），α∈[0，π]
∴
=（2-2cosα，4-2sinα），
=（-2-2cosα，4-2sinα），
由此可得
•
=（2-2cosα）（-2-2cosα）+（4-2sinα）（4-2sinα）
=4cos2α-4+16-16sinα+4sin2α=16-16sinα
化简得
•
=16-16sinα
∵α∈[0，π]，sinα∈[0，1]
∴当α=0或π时，
•
取最大值为16；当α=
时，
•
取最小值为0．
由此可得
•
的取值范围是[0，16]
故答案为：[0，16]
解：以AB中点为坐标原点，AB所在直线为x轴建立如图坐标系则圆弧APB方程为x2+y2=4，（y≥0），C（2，4），D（-2，4）
因此设P（2cosα，2sinα），α∈[0，π]
∴
| PC |
| PD |
由此可得
| PC |
| PD |
=4cos2α-4+16-16sinα+4sin2α=16-16sinα
化简得
| PC |
| PD |
∵α∈[0，π]，sinα∈[0，1]
∴当α=0或π时，
| PC |
| PD |
| π |
| 2 |
| PC |
| PD |
由此可得
| PC |
| PD |
故答案为：[0，16]
点评：本题给出正方形内半圆上一个动点，求向量数量积的取值范围，着重考查了平面向量数量积的运算性质和圆的参数方程等知识，属于中档题．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
如图，ABCD是边长为3的正方形，DE⊥平面ABCD，AF∥DE，DE=3AF，BE与平面ABCD所成角为60°．
如图，ABCD是边长为a的菱形，且∠BAD=60°，△PAD为正三角形，且面PAD⊥面ABCD．
如图，ABCD是边长为2的正方形，面EAD⊥面ABCD，且EA=ED，EF∥AB，且EF=1，O是线段AD的中点，三棱锥F-OBC的体积为
（2012•宁城县模拟）如图，ABCD是边长为1的正方形，DE⊥平面ABCD，AF∥DE，DE=2AF．
如图，ABCD是边长为2的正方形纸片，沿某动直线l为折痕将正方形在其下方的部分向上翻折，使得每次翻折后点B都落在边AD上，记为B'；折痕与AB交于点E，以EB和EB’为邻边作平行四边形EB’MB．若以B为原点，BC所在直线为x轴建立直角坐标系（如下图）：