题目内容
设函数f（x）=sinx+cosx，函数h（x）=f（x）f′（x），下列说法正确的是
- A.y=h（x）在（0，
）单调递增，其图象关于直线x=
对称 - B.y=h（x）在（0，）单调递增，其图象关于直线x=对称
- C.y=h（x）在（0，）单调递减，其图象关于直线x=对称
- D.y=h（x）在（0，）单调递减，其图象关于直线x=对称
D
分析：先化简函数，再利用余弦函数的性质，可得结论．
解答：由题意，h（x）=f（x）f′（x）=（cosx+sinx）（cosx-sinx）=cos2x
∴y=h（x）在（0，）单调递减，其图象关于直线x=对称
故选D．
点评：本题考查三角函数图象和性质，属于中等题．
分析：先化简函数，再利用余弦函数的性质，可得结论．
解答：由题意，h（x）=f（x）f′（x）=（cosx+sinx）（cosx-sinx）=cos2x
∴y=h（x）在（0，
）单调递减，其图象关于直线x=对称故选D．
点评：本题考查三角函数图象和性质，属于中等题．
练习册系列答案
相关题目
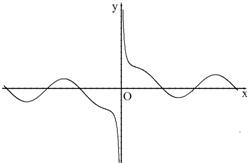如图是函数Q（x）的图象的一部分，设函数f（x）=sinx，g （ x ）=| 1 |
| x |
A、
| ||
| B、f（x）g（x） | ||
| C、f（x）-g（x） | ||
| D、f（x）+g（x） |
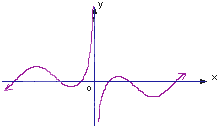设函数f（x）=sinx，g（x）=