题目内容
19. 设函数 (1)若![]() 处取得极值,求常数a的值;
处取得极值,求常数a的值;
(2)若![]() 上为增函数,求a的取值范围.
上为增函数,求a的取值范围.
19. 解:(Ⅰ)![]()
因![]() 取得极值,所以
取得极值,所以![]()
解得![]()
经检验知当![]() 为极值点.
为极值点.
(Ⅱ)令![]()
当a<1时,若x∈(-∞,a)∪(1,+∞),则f′(x)>0,所以f(x)在(-∞,a)和(1,+∞)上为函数,故当![]() 上为增函数.
上为增函数.
当a≥1时,若x∈(-∞,1)∪(a ,+∞),则f′(x)>0,所以f(x)在(-∞,1)和(a,+∞)为增函数,从而![]() 上也为增函数.
上也为增函数.
综上所述,当![]() 上为增函数.
上为增函数.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 R.
R.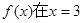 处取得极值,求常数
处取得极值,求常数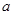 的值;
的值;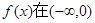 上为增函数,求
上为增函数,求