题目内容
12. 如图,点P是正方形ABCD外一点,PA⊥平面ABCD,PA=AB=2,且E,F分别是AB,PC的中点.
如图,点P是正方形ABCD外一点,PA⊥平面ABCD,PA=AB=2,且E,F分别是AB,PC的中点.(1)求证:EF⊥平面PCD;
(2)求直线BD与平面EFC所成角的正弦值.
分析 (1)根据已知条件利用做线段的中点,利用三角形的中位线,得到线线垂直,进一步转化成线面垂直,再利用等腰三角形的性质,得到线线垂直,最后得到线面垂直.
(2)首先建立空间直角坐标系,利用线段的长求出空间点的坐标,进一步利用法向量知识最后求出线面的夹角的正弦值.
解答 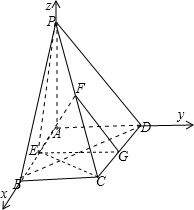 证明:(1)点P是正方形ABCD外一点,E,F分别是AB,PC的中点.
证明:(1)点P是正方形ABCD外一点,E,F分别是AB,PC的中点.
取CD的中点G,连接FG,EG,
所以:FG∥PD,
PA⊥平面ABCD,
所以:PA⊥CD,
由于四边形ABCD为正方形,
所以:CD⊥AD
则:CD⊥平面PAD,
所以:CD⊥PD,
在平面PCD中,FG∥PD,
所以:FG⊥CD.
由于E、G是AB和CD的中点,
所以:EG⊥CD,
则:CD⊥平面EFG,
所以EF⊥CD.
连接PE和CE,PA=AB=2,
利用勾股定理得到:EP=EC=$\sqrt{5}$
F是PC的中点,
则:△EPC为等腰三角形.
所以:EF⊥PC.
由于:EF⊥CD,
所以:EF⊥平面PCD.
(2)建立空间直角坐标系A-xyz,则根基题中已知条件:
则:B(2,0,0),D(0,2,0),E(1,0,0),F(1,1,1),C(2,2,0),
所以:$\overrightarrow{EF}=(0,1,1)$,$\overrightarrow{CF}=(-1,-1,1)$,$\overrightarrow{BD}=(-2,2,0)$,
设平面CEF的法向量为:$\overrightarrow{n}=(x,y,z)$
所以:$\left\{\begin{array}{l}\overrightarrow{EF}•\overrightarrow{n}=0\\ \overrightarrow{CF}•\overrightarrow{n}=0\end{array}\right.$
即:$\left\{\begin{array}{l}y+z=0\\-x-y+z=0\end{array}\right.$
解得:$\overrightarrow{n}=(2,-1,1)$
设直线BD与平面EFC所成角为θ,
则sinθ=$cos<\overrightarrow{BD},\overrightarrow{n}>$=$\left|\frac{\overrightarrow{BD}•\overrightarrow{n}}{\left|\overrightarrow{BD}\right|\left|\overrightarrow{n}\right|}\right|$=$\frac{\sqrt{3}}{3}$.
点评 本题考查的知识要点:线面垂直的判定和性质定理的应用,空间直角坐标系,法向量的应用,线面的夹角的应用,向量的角角公式的应用,及相关的运算问题.

| A. | 在圆内 | B. | 在圆外 | C. | 在圆上 | D. | 不能确定 |
| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是①②④⑤(写出所有正确命题的编号).
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是①②④⑤(写出所有正确命题的编号).