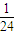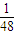题目内容
在区域M={（x，y）|0＜x＜π，0＜y＜2}内随机撒一把黄豆，落在区域N={(x ，y)|y＜| πx-x2 |
分析：先明确概率类型为几何概型中的面积类型，则先求出区域M={（x，y）|0＜x＜π，0＜y＜2}的面积，再求得区域N={(x ，y)|y＜
}的面积，再由几何概型的概率公式求解．
| πx-x2 |
解答：解：区域M={（x，y）|0＜x＜π，0＜y＜2}的面积为：2π
区域N={(x ，y)|y＜
}的面积为：
∴落在区域N={(x ，y)|y＜
}内的概率是
=
故答案为：
区域N={(x ，y)|y＜
| πx-x2 |
| π3 |
| 8 |
∴落在区域N={(x ，y)|y＜
| πx-x2 |
| ||
| 2π |
| π2 |
| 16 |
故答案为：
| π2 |
| 16 |
点评：本题主要考查几何概型中面积类型，方法是分别求得相应的面积，再求相应的比值．
练习册系列答案
相关题目
}，某人向区域M随机投掷一点P，则点P正好落在区域N的概率为
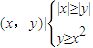}，某人向区域M随机投掷一点P，则点P正好落在区域N的概率为（ ）
