题目内容
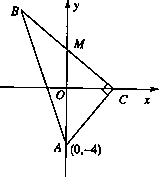
如图,P为直角三角形ABC所在平面α外一点,∠C= ,PC=24,P到两条直角边的距离都是6
,PC=24,P到两条直角边的距离都是6 ,求:
,求:

(1)P到平面α的距离;
(2)PC与平面α所成的角.
答案:
解析:
解析:
|
作PO⊥α于点O,过O作OD⊥BC,OE⊥AC,D、E为垂足,连接PD、PE,由三垂线定理知BC⊥PD,AC⊥PE,则PD=PE=6
在Rt△PCO中,可求PC与平面α所成的角为∠PCO= |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,于是OD=OE,又∠C=
,于是OD=OE,又∠C= ,则四边形OECD为正方形,在Rt△PCE中,CE=OE=
,则四边形OECD为正方形,在Rt△PCE中,CE=OE= 在Rt△POE中可求PO=12为所求.
在Rt△POE中可求PO=12为所求.
 .
. 如图,在等腰直角三角形ABC中,AC=BC=1,点M,N分别是AB,BC的中点,点P是△ABC(包括边界)内任一点.则
如图,在等腰直角三角形ABC中,AC=BC=1,点M,N分别是AB,BC的中点,点P是△ABC(包括边界)内任一点.则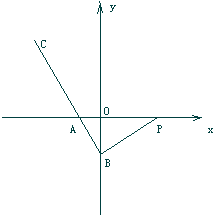 如图,已知直角三角形PAB的直角顶点为B,点P的坐标为(3,0),点B在y轴上,点A在x轴的负半轴上,在BA的延长线上取一点C,使
如图,已知直角三角形PAB的直角顶点为B,点P的坐标为(3,0),点B在y轴上,点A在x轴的负半轴上,在BA的延长线上取一点C,使 (2013•广州二模)如图,一个等腰直角三角形的直角边长为2,分别以三个顶点为 圆心,l为半径在三角形内作圆弧,三段圆弧与斜边围成区域M (图中白色部分).若在此三角形内随机取一点P,则点P落在区 域M内的概率为
(2013•广州二模)如图,一个等腰直角三角形的直角边长为2,分别以三个顶点为 圆心,l为半径在三角形内作圆弧,三段圆弧与斜边围成区域M (图中白色部分).若在此三角形内随机取一点P,则点P落在区 域M内的概率为