Question

12．一副纸牌共52张，其中“方块”“梅花”“红心”“黑桃”每种花色的牌各13张，标号依次是2，3，…10，J，Q，K，A，其中相同花色，相邻标号的两张牌称为“同花顺牌”，并且A与2也算是顺牌（即A可以当成1使用）．试确定，从这副牌中取出13张牌，使每种标号的牌都出现，并且不含“同花顺牌”的取牌种数．

Answer 1

分析 将问题转化为一般问题：设n≥3，从A={a₁，a₂，a₃，…a_n}，B={b₁，b₂，b₃，…b_n}，C={c₁，c₂，c₃，…c_n}，D={d₁，d₂，d₃，…d_n}，这四个数列中选取n个项，且满足：①1，2，…，每个下标都出现；②下标相邻的任两项不在同一个数列中（下标n与1视为相邻），其选取方法数记为x_n，今确定x_n的运算式即可．

解答 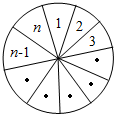解：先一般化为下述问题：设n≥3，从A={a₁，a₂，a₃，…a_n}，B={b₁，b₂，b₃，…b_n}，C={c₁，c₂，c₃，…c_n}，D={d₁，d₂，d₃，…d_n}，
这四个数列中选取n个项，且满足：
①1，2，…，每个下标都出现；
②下标相邻的任两项不在同一个数列中（下标n与1视为相邻），其选取方法数记为x_n，今确定x_n的运算式；
将一个圆盘分成n个扇形格，顺次编号为1，2…，并将数列A，B，C，D，各染一种颜色，对于任一个选项方案，如果下标为i的项取自某颜色数列，则将第i号扇形格染上该颜色，
于是x_n就成为将圆盘的n个扇形格染四色，使相邻格不同色的染色方法数，易知，x₁=4，x₂=12，
x_n+x_n-1=4•3^n-1，（n≥3），（1）
将（1）写作（-1）ⁿx_n-（-1）^n-1x_n-1=-4•（-3）^n-1，
因此（-1）^n-1x_n-（-1）^n-2x_n-1=-4•（-3）^n-2，
…
（-1）³x₃-（-1）²x₂=-4•（-3）²，
（-1）²x₂=-4•（-3），
相加得（-1）ⁿx_n=3+（-3）ⁿ，
于是x_n=3ⁿ+3•（-1）ⁿ，（n≥2），
当n=13时，x₁₃=3¹³-3．

点评 本题主要考查与数列有关的计算问题，根据条件构造数列，利用累加法是解决本题的关键．综合性较强，难度较大，是一个难度较大的竞赛试题．