题目内容
5.若实数x,y满足$\left\{\begin{array}{l}{x-y≤0}\\{x+y-4≤0}\\{x≥0}\end{array}\right.$,则|3x+y-4|+|x+2y+8|的最小值是( )| A. | 11 | B. | 12 | C. | 16 | D. | 18 |
分析 作出不等式组对应的平面区域,利用数形结合进行求解即可.
解答 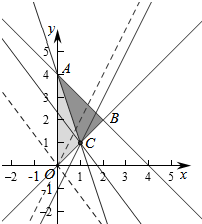 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
则由图象知,x≥0,y≥0,则|x+2y+8|=x+2y+8,
设z=|3x+y-4|+|x+2y+8|,
则z=|3x+y-4|+x+2y+8,
若3x+y-4≥0,则不等式对应的区域为△ACB,
此时z=3x+y-4+x+2y+8=4x+3y+4,
即y=$-\frac{4}{3}$x+$\frac{z-4}{3}$,平移直线y=$-\frac{4}{3}$x+$\frac{z-4}{3}$由图象知当直线y=$-\frac{4}{3}$x+$\frac{z-4}{3}$经过点C时,直线y=$-\frac{4}{3}$x+$\frac{z-4}{3}$的截距最小,此时z最小,
由$\left\{\begin{array}{l}{3x+y-4=0}\\{x-y=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,即C(1,1),此时z=4+3+4=11,
若3x+y-4≤0,则不等式对应的区域为△OAC,
此时z=-(3x+y-4)+x+2y+8=-2x+y+12,
即y=2x+z-12,平移直线y=2x+z-12,由图象知当直线y=2x+z-12,经过点C时,直线y=2x+z-12的截距最小,此时z最小,
此时z=-2+1+12=11,
综上|3x+y-4|+|x+2y+8|的最小值是11.
故选:A.
点评 本题主要考查线性规划的应用,作出不等式组对应的平面区域,根据绝对值的性质,利用数形结合是解决本题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
16.若函数f(x)=$\frac{x+2}{m{x}^{2}+2mx+3}$的定义域为R,则实数m的取值范围是 ( )
| A. | (0,3) | B. | [0,3) | C. | [0,2)∪(2,3) | D. | [0,2)∪(2,3] |
17.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2.|$\overrightarrow{c}$|=1.$\overrightarrow{a}$•$\overrightarrow{b}$=1,则($\overrightarrow{a}$-$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{c}$)的最大值为 ( )
| A. | 2+$\sqrt{10}$ | B. | 2+$\sqrt{7}$ | C. | 1+$\sqrt{10}$ | D. | 1+$\sqrt{7}$ |
15.已知a,b是两条不同的直线.α,β,γ是三个不重合的平面,则下列命题为真命题的是( )
| A. | 若a∥α,α⊥β,则a⊥β | |
| B. | 若a,b与α所成角相等,则a∥b | |
| C. | 若α⊥β,γ⊥β,则α∥γ | |
| D. | 若a,b为异面直线,a?α,a∥β,b?β,b∥α,则α∥β |
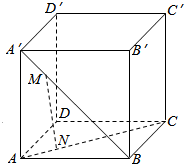 在正方体ABCD-A′B′C′D中,M,N分别是A′B,AC上的点,且A′M=AN,求证:MN∥平面BB′CC′.
在正方体ABCD-A′B′C′D中,M,N分别是A′B,AC上的点,且A′M=AN,求证:MN∥平面BB′CC′.