题目内容
已知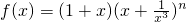
（n∈N*）．
（1）当n=8时，求f（x）展开式中的常数项；
（2）若f（x）展开式中没有常数项，且2＜n＜6，求n的值，并求此时f（x）展开式中含x2项的系数．
解：解：（1）当n=8时，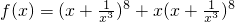
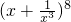的通项为C8rx8-4r，
当r=2时为常数项C82=28
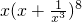的通项为C8kx9-4k，无常数项
故f（x）展开式中常数项为28
（2）
=
+
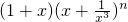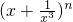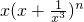
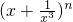的通项为Cnrxn-4r，无常数项，故n≠4
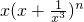的通项为Cnkxn-4k+1，无常数项．故n≠4k-1
由于n∈N*且2＜n＜6，
故n=5
当n=5时，x2项的系数求解如下：5-4r=2无解；
5-4k+1=2，故k=1，所以x2项的系数为C51=5．
分析：（1）将n的值代入f（x），利用多项式的乘法展开，利用二项展开式的通项公式求出两部分的通项，令x的指数为0求出r的值，代入通项求出展开式的常数项．
（2）按多项式的乘法展开，利用二项展开式的通项公式求出两部分的通项，令x的指数不为0，在n的范围内求出n，将n的值代入通项，令x的指数为2，求出展开式中含x2项的系数．
点评：解决二项展开式的特定项的问题，一般利用二项展开式的通项公式求出展开式的通项，再解决．
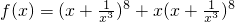
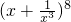的通项为C8rx8-4r，当r=2时为常数项C82=28
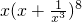的通项为C8kx9-4k，无常数项故f（x）展开式中常数项为28
（2）
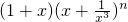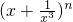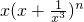
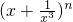=+的通项为Cnrxn-4r，无常数项，故n≠4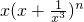的通项为Cnkxn-4k+1，无常数项．故n≠4k-1由于n∈N*且2＜n＜6，
故n=5
当n=5时，x2项的系数求解如下：5-4r=2无解；
5-4k+1=2，故k=1，所以x2项的系数为C51=5．
分析：（1）将n的值代入f（x），利用多项式的乘法展开，利用二项展开式的通项公式求出两部分的通项，令x的指数为0求出r的值，代入通项求出展开式的常数项．
（2）按多项式的乘法展开，利用二项展开式的通项公式求出两部分的通项，令x的指数不为0，在n的范围内求出n，将n的值代入通项，令x的指数为2，求出展开式中含x2项的系数．
点评：解决二项展开式的特定项的问题，一般利用二项展开式的通项公式求出展开式的通项，再解决．
练习册系列答案
相关题目
已知n∈N*，则不等式|
-2|＜0.01的解集为（ ）
| 2n |
| n+1 |
| A、{n|n≥199，n∈N*} |
| B、{n|n≥200，n∈N*} |
| C、{n|n≥201，n∈N*} |
| D、{n|n≥202，n∈N*} |
