题目内容
 若0≤θ≤
若0≤θ≤| π |
| 2 |
| 2 |
1
1
.分析:由点到直线的距离公式可得sinθ+cosθ=±
,由两角和与差的三角函数公式可得sin(θ+
)=±1,结合题目给的范围可得θ=
,求其正切值即可.
| 2 |
| π |
| 4 |
| π |
| 4 |
解答:解:由点到直线的距离公式可得:
=
,即sinθ+cosθ=±
,
故
sinθ+
cosθ=±1,即sin(θ+
)=±1,
又0≤θ≤
,故θ=
,
故直线的向量为tan
=1
故答案为:1
| |sinθ+cosθ| | ||
|
| 2 |
| 2 |
故
| ||
| 2 |
| ||
| 2 |
| π |
| 4 |
又0≤θ≤
| π |
| 2 |
| π |
| 4 |
故直线的向量为tan
| π |
| 4 |
故答案为:1
点评:本题考查点到直线的距离公式,涉及和与差的三角函数公式,属基础题.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
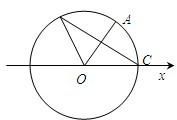 如图,A、B是单位圆O上的动点,C是圆与x轴正半轴的交点,设∠COA=α.
如图,A、B是单位圆O上的动点,C是圆与x轴正半轴的交点,设∠COA=α.