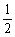题目内容
如下图,在梯形ABCD中,CD∥AB,AD=DC=BC=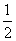 AB=a,E是AB的中点,将△ADE沿DE折起,使点A折起到点P的位置,使二面角P-DE-C的大小为120°,
AB=a,E是AB的中点,将△ADE沿DE折起,使点A折起到点P的位置,使二面角P-DE-C的大小为120°,
(1)求证:DE⊥PC;
(2)求直线PD与平面BCDE所成角的正弦值.
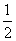 AB=a,E是AB的中点,将△ADE沿DE折起,使点A折起到点P的位置,使二面角P-DE-C的大小为120°,
AB=a,E是AB的中点,将△ADE沿DE折起,使点A折起到点P的位置,使二面角P-DE-C的大小为120°,(1)求证:DE⊥PC;
(2)求直线PD与平面BCDE所成角的正弦值.
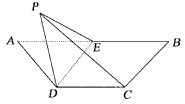
| (1)证明:在梯形ABCD中,连结CE,则易知四边形ADCE为菱形, 连接AC交DE于F,则AC⊥DE, 连接PF,则PF⊥DE, 又AC∩PF=F, ∴DE⊥平面PCF, ∴DE⊥PC。 (2)解:过点P作PO⊥平面ADE,则易知点O在AC上,连接OD, 则∠PDO即为直线PD与平面BCDE所成的角, ∵二面角P-DE-C的大小为120°,且可知∠PFC即为二面角的平面角, ∴∠PFO=60°, 又PF=  a, a,∴OP=  a, a,∴  。 。 |
 |

练习册系列答案
相关题目