题目内容
如图,两块全等的直角边长为1的等腰直角三角形拼在一起,若![]() D=
D=![]() B+k
B+k![]() C,则λ+k=( )
C,则λ+k=( )

|
| A. |
| B. |
| C. | 2 | D. |
|
考点:
向量在几何中的应用.
专题:
计算题;平面向量及应用.
分析:
如图,以A为原点,AB、AC所在直线分别为x、y轴建立直角坐标系,可得A、B、C、D各点的坐标,从而得到向量![]() 、
、![]() 坐标,结合题意可算出λ和k的值,进而得到λ+k的值.
坐标,结合题意可算出λ和k的值,进而得到λ+k的值.
解答:
解:以A为原点,AB、AC所在直线分别为x、y轴建立如图直角坐标系,可得
A(0,0),B(1,0),C(0,1)
∵△ABC、△CDE是直角边长为1的等腰直角三角形
∴![]() =(
=(![]() ,
,![]() )
)
因此,向量![]() =
=![]() +
+![]() =(0,1)+(
=(0,1)+(![]() ,
,![]() )=(
)=(![]() ,1+
,1+![]() )
)
∵![]() =
=![]() =λ(1,0)+k(0,1)=(λ,k)
=λ(1,0)+k(0,1)=(λ,k)
∴λ=![]() ,k=1+
,k=1+![]() ,可得λ+k=1+
,可得λ+k=1+![]()
故选:A

点评:
本题给出两个全等的等腰直角三角形,在已知向量等式的情况下求λ+k的值.着重考查了平面向量的线性运算、坐标运算和向量在几何中的应用等知识,属于基础题.

练习册系列答案
相关题目
 如图,两块全等的直角边长为1的等腰直角三角形拼在一起,若
如图,两块全等的直角边长为1的等腰直角三角形拼在一起,若 如图,两块全等的直角边长为1的等腰直角三角形拼在一起,若
如图,两块全等的直角边长为1的等腰直角三角形拼在一起,若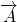 D=
D= B+k
B+k
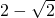
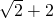
 D=
D= B+k
B+k C,则λ+k=( )
C,则λ+k=( )



 D=
D= B+k
B+k C,则λ+k=( )
C,则λ+k=( )


