题目内容
【题目】已知数列![]() 与
与![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)设![]() 的第
的第![]() 项是最大项,即
项是最大项,即![]() ,求证:
,求证:![]() 的第
的第![]() 项是最大项;
项是最大项;
(3)设![]() ,求
,求![]() 的取值范围,使得
的取值范围,使得![]() 有最大值
有最大值![]() 与最小值
与最小值![]() ,且
,且![]() .
.
【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】
(1)把bn=3n+5代入已知递推式可得an+1﹣an=6,由此得到{an}是等差数列,则an可求;
(2)由an=(an﹣an﹣1)+(an﹣1﹣an﹣2)+…+(a2﹣a1)+a1,结合递推式累加得到an=2bn+a1﹣2b1,求得![]() ,进一步得到
,进一步得到![]() 得答案;
得答案;
(3)由(2)可得![]() ,然后分﹣1<λ<0,λ=﹣1,λ<﹣1三种情况求得an的最大值M和最小值m,再由
,然后分﹣1<λ<0,λ=﹣1,λ<﹣1三种情况求得an的最大值M和最小值m,再由![]() ∈(﹣2,2)列式求得λ的范围.
∈(﹣2,2)列式求得λ的范围.
(1)由![]() 可得:
可得:![]() ,又
,又![]() ,所以数列
,所以数列![]() 以1为首项,6为公差的等差数列,即有
以1为首项,6为公差的等差数列,即有![]() ;
;
(2)由![]() 可得:
可得:
![]()
![]()
……
![]() ,
,
将上述式子累加可得
![]() ,当
,当![]() 时,也成立,所以
时,也成立,所以![]() ,由此可得
,由此可得
![]() ,由于
,由于![]() 为常数,所以当
为常数,所以当![]() 的第
的第![]() 项是最大项时,
项是最大项时,![]() 最大,即
最大,即![]() 的第
的第![]() 项是最大项;
项是最大项;
(3)由(2)可知![]() ,即
,即![]() ,结合
,结合![]() 可得
可得
![]() ,分三种情况进行讨论:
,分三种情况进行讨论:
①当![]() 时,则
时,则![]() 为偶数时
为偶数时![]() ,
,![]() 为奇数时,
为奇数时,![]() ,即
,即![]() ,此时
,此时![]() ,由此,此情况不符合条件;
,由此,此情况不符合条件;
②当![]() 时,则
时,则![]() 为偶数时,
为偶数时,![]() ,由于
,由于![]() ,所以
,所以![]() ,从而
,从而![]() “随着
“随着![]() 增大值减小,此时
增大值减小,此时![]() ,
,![]() ,无最小值(无限靠近0);
,无最小值(无限靠近0);![]() 为奇数,
为奇数,![]() ,此时
,此时![]() ,由于
,由于![]() ,所以
,所以![]() ,从而
,从而![]() 随着
随着![]() 增大值减小,结合
增大值减小,结合![]() ,可知随着
,可知随着![]() 增大
增大![]() 值增大,此时
值增大,此时![]() ,无最大值(无限靠近0);由此可知数列
,无最大值(无限靠近0);由此可知数列![]() 的最大值
的最大值![]() ,最小值
,最小值![]() ,
,![]() ,又
,又![]() ,所以
,所以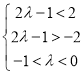 ,解之
,解之![]() ;
;
③当![]() 时,则
时,则![]() 为偶数时,
为偶数时,![]() ,由于
,由于![]() ,所以
,所以![]() ,从而
,从而![]() 随着
随着![]() 增大值增大,此时
增大值增大,此时![]() ,
,![]() ,无最大值(无限靠近
,无最大值(无限靠近![]() );
);![]() 为奇数时,
为奇数时,![]() ,此时
,此时![]() ,由于
,由于![]() ,所以
,所以![]() ,从而
,从而![]() 随着
随着![]() 增大值增大,结合
增大值增大,结合![]() ,可知随着
,可知随着![]() 增大
增大![]() 值减小,此时
值减小,此时![]() ,无最小值(无限靠近
,无最小值(无限靠近![]() );由此可知,在
);由此可知,在![]() 条件下,数列
条件下,数列![]() 无最值,显然不符合条件;
无最值,显然不符合条件;
综上,符合条件的实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目