Question

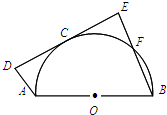如图AB为半圆的直径，DE为半圆的一条切线，点C为切点，AD⊥DE于D，BE⊥DE于E交半圆于F，若AD=3，BE=7，那么线段DE的长为

2

21

．

Answer 1

分析：连接OC，由已知中DE为半圆的一条切线，点C为切点，AD⊥DE于D，BE⊥DE于E，可得OC⊥DE，结合O为直径AB的中点O，可得OC为梯形ABED的中位线，即半圆的半径为5，连接AF，解直角三角形ABF，可得AF的长，即DE的长．

解答：解：连接OC，
由O是AB的中点，OC⊥DE，AD⊥DE于D，BE⊥DE于E
可得CO为梯形ABED的中位线
∴OC=

1

2

（AD+BE）=5
连接AF
在Rt△ABF中，AB=2OC=10，BF=BE-AD=4
故AF=

AB2-BF2

=2

21

故DE=AF=2

21

故答案为2

21

点评：本题考查的知识点是圆的切线的性质定理的证明，圆周角定理，其中根据已知计算出OC即半圆半径的长，是解答本题的关键．