题目内容
 如图,AB为半圆的直径,P为半圆上一点,|AB|=10,∠PAB=a,且sina=
如图,AB为半圆的直径,P为半圆上一点,|AB|=10,∠PAB=a,且sina= ,建立适当的坐标系.
,建立适当的坐标系.
(1)求A、B为焦点且过P点的椭圆的标准方程.
(2)动圆M过点A,且与以B为圆心,以2 为半径的圆相外切,求动圆圆心M的轨迹方程.
为半径的圆相外切,求动圆圆心M的轨迹方程.
解:(1)以直线AB为x轴,线段AB的垂直平分线为y轴,建立直角坐标系.
∵AB为半圆的直径,P为半圆上一点,∴∠APB=90°.
在Rt△APB中,|PB|=|AB|sinα= =8,∴|AP|=6.
=8,∴|AP|=6.
∴|PA|+|PB|=6+8=14=2a,解得a=7,
∵2c=10,∴c=5,
∴b2=a2-c2=24.
∴椭圆的标准方程为: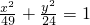 .
.
(2)由题意可得:|MB|-|MA|= <10=|AB|,
<10=|AB|,
故动圆圆心M的轨迹在双曲线的左支上,
∵2c′=10,2a′= ,∴c′=5,a′=
,∴c′=5,a′= ,
, .
.
其方程为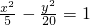
 .
.
分析:(1)建立如图所示的直角坐标系,利用直角三角形的边角关系即可得到|PB|,利用勾股定理即可得到|PA|,从而得到2a,|AB|=2c,再利用b2=a2-c2即可得到椭圆的标准方程.
(2)利用两圆外切的性质和双曲线的定义即可得出.
点评:熟练掌握圆锥曲线的定义和性质、两圆外切的性质、勾股定理是解题的关键.

∵AB为半圆的直径,P为半圆上一点,∴∠APB=90°.
在Rt△APB中,|PB|=|AB|sinα=
 =8,∴|AP|=6.
=8,∴|AP|=6.∴|PA|+|PB|=6+8=14=2a,解得a=7,
∵2c=10,∴c=5,
∴b2=a2-c2=24.
∴椭圆的标准方程为:
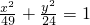 .
.(2)由题意可得:|MB|-|MA|=
 <10=|AB|,
<10=|AB|,故动圆圆心M的轨迹在双曲线的左支上,
∵2c′=10,2a′=
 ,∴c′=5,a′=
,∴c′=5,a′= ,
, .
.其方程为
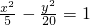
 .
.分析:(1)建立如图所示的直角坐标系,利用直角三角形的边角关系即可得到|PB|,利用勾股定理即可得到|PA|,从而得到2a,|AB|=2c,再利用b2=a2-c2即可得到椭圆的标准方程.
(2)利用两圆外切的性质和双曲线的定义即可得出.
点评:熟练掌握圆锥曲线的定义和性质、两圆外切的性质、勾股定理是解题的关键.

练习册系列答案
相关题目
