题目内容
数列{an}满足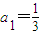
，且对于任意的正整数m，n都有
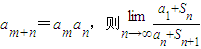=（ ）A．
B．
C．1
D．
【答案】分析：确定数列{an}为等比数列，进而表示出数列的前n项和，最后求极限，可得出答案．
解答：解：令m=1，则∵am+n=am•an，∴a1+n=a1•an，
∵
，∴
∴数列{an}是首项为
，公比为
的等比数列．
∴
=
∴
=
=
=
故选A．
点评：本题考查了等比数列关系的确定，考查等比数列的前n项和的公式及会进行极限的运算，是一道综合题．
解答：解：令m=1，则∵am+n=am•an，∴a1+n=a1•an，
∵
，∴∴数列{an}是首项为
，公比为的等比数列．∴
=∴
===故选A．
点评：本题考查了等比数列关系的确定，考查等比数列的前n项和的公式及会进行极限的运算，是一道综合题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
=ad-bc,若数列{an}满足
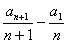=1,且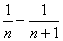
=2(n∈N*)，则a10为（ ）
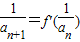，且a1=4，求数列an的通项公式；
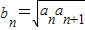，数列bn的前n项和Tn，求证：
．
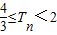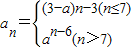且{an}是递增数列，则实数a的范围是（ ）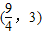
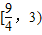
，且a1=4，求数列{an} 的通项公式；
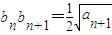，当n≥3，n∈N*时，求证：①
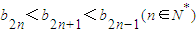；②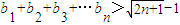
．
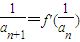，且a1=4，求数列an的通项公式；
，数列bn的前n项和Tn，求证：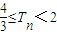
．