题目内容
已知二次函数f（x）=ax2+bx的图象过点（-4n，0），且f'（0）=2n，n∈N*．（Ⅰ）求f（x）的解析式；
（Ⅱ）若数列an满足
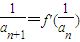，且a1=4，求数列an的通项公式；（Ⅲ）记
，数列bn的前n项和Tn，求证：
．
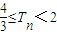【答案】分析：（I）根据二次函数f（x）=ax2+bx的图象过点（-4n，0），且f'（0）=2n建立方程组，解之即可求出f（x）的解析式；
（II）由条件得
，然后利用累加得
的通项公式，从而求出an的通项公式；
（III）先根据条件求出bn的通项公式，然后利用裂项求和法进行求和求出Tn，而2n+1≥3，从而证得
．
解答：解：（I）由
解之得
（II）由条件得
，
∴
，累加得；
∴
（n≥2）
当n=1时，a1=2≠4不满足上面的通项公式
则
（III）
∵
点评：本题主要考查了数列与函数的综合应用，同时考查了叠加法和裂项求和法的运用，属于中档题．
（II）由条件得
，然后利用累加得的通项公式，从而求出an的通项公式；（III）先根据条件求出bn的通项公式，然后利用裂项求和法进行求和求出Tn，而2n+1≥3，从而证得
．解答：解：（I）由
解之得
（II）由条件得
，∴
，累加得；∴
（n≥2）当n=1时，a1=2≠4不满足上面的通项公式
则
（III）
∵
点评：本题主要考查了数列与函数的综合应用，同时考查了叠加法和裂项求和法的运用，属于中档题．
练习册系列答案
相关题目