题目内容
12.已知c>0,设命题p:函数y=cx为减函数.命题q:函数f(x)=cx2-x+c在区间$[{\frac{1}{2},2}]$上恒大于零.若命题“p∨q”为真命题,命题“p∧q”为假命题,求实数c的取值范围.分析 分别求出p,q为真时的c的范围,根据p,q一真一假得到关于c的不等式组,解出即可.
解答 解:由命题p为真可知,0<c<1,
由命题q为真可知,
$\left\{\begin{array}{l}{\frac{1}{2c}≤\frac{1}{2}}\\{f(\frac{1}{2})>0}\end{array}\right.$或$\left\{\begin{array}{l}{\frac{1}{2c}≥2}\\{f(2)≥0}\end{array}\right.$或△=1-4c2>0,
∴$c>\frac{1}{2}$,
由题意得,p,q一真一假,
∴$\left\{\begin{array}{l}{0<c<1}\\{c≤\frac{1}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{c≥1}\\{c>\frac{1}{2}}\end{array}\right.$,
∴$0<c≤\frac{1}{2}或c≥1$.
点评 本题考查了复合命题的判断,考查二次函数、指数函数的性质,是一道基础题.

练习册系列答案
相关题目
7.若在区间(-1,1)任取实数a,则直线ax-y=0与圆(x-1)2+(y-2)2=1相交的概率为( )
| A. | $\frac{5}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{16}$ | D. | $\frac{1}{4}$ |
17.偶函数f(x)在区间[1,4]上为减函数,则它在区间[-4,-1]上( )
| A. | 是增函数 | B. | 是减函数 | C. | 无法确定 | D. | 不具备单调性 |
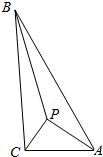 如图,在△ABC中,∠C=90°,P为三角形内一点,且S△PAB=S△PBC=S△PCA,求证:|PA|2+|PB|2=5|PC|2.
如图,在△ABC中,∠C=90°,P为三角形内一点,且S△PAB=S△PBC=S△PCA,求证:|PA|2+|PB|2=5|PC|2.