题目内容

求函数y=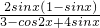 $数学公式$ ，x∈（0， $数学公式$ ）的值域．

解：y= $\text{[math]}$ = $\text{[math]}$ ．
设t=sinx，则由x∈（0， $\text{[math]}$ ）?t∈（0，1）．
对于y= $\text{[math]}$ = $\text{[math]}$
=-1+ $\text{[math]}$ - $\text{[math]}$ ，
令 $\text{[math]}$ =m，m∈（ $\text{[math]}$ ，1），
则y=-2m²+3m-1=-2（m- $\text{[math]}$ ）²+ $\text{[math]}$ ．
当m= $\text{[math]}$ ∈（ $\text{[math]}$ ，1）时，y_max= $\text{[math]}$ ，
当m= $\text{[math]}$ 或m=1时，y=0．
∴0＜y≤ $\text{[math]}$ ，即函数的值域为y∈（0， $\text{[math]}$ ]．
分析：将原函数中不同名的三角函数都化成单角的正弦函数，再换元将其转化为熟悉的一元二次函数求解．
点评：本题的解法较多，此种解法主要体现了换元转化的思想，在换元时要注意变量的范围．

练习册系列答案

金牌教练赢在燕赵系列答案

0系列答案

金题金卷热点测试系列答案

金钥匙试卷系列答案

金钥匙知识训练营系列答案

金指课堂同步检评系列答案

锦囊妙解系列答案

经典创新高分拔尖训练系列答案

精编精练提优作业本系列答案

精典练习系列答案

相关题目

已知函数f(x)=

sinωx+cos(ωx+

)-1(ω＞0，x∈R)，且函数f（x）的最小正周期为π．
（I）求函数f（x）的解析式；
（Ⅱ）将函数f（x）昀图象向右平移

个单位，得到函数了y=g（x）的图象，求函数y=g(x)在[0，

]上的值域．

已知函数f(x)=

sinωx+cos(ωx+

)-1(ω＞0，x∈R)，且函数f（x）的最小正周期为π．
（I）求函数f（x）的解析式；
（Ⅱ）将函数f（x）昀图象向右平移

个单位，得到函数了y=g（x）的图象，求函数y=g(x)在[0，

]上的值域．

（本小题12分）

已知函数f(x)=x－（2a+1）x+3a（a+2）x+，其中a为实数。

（1）当a=－1时，求函数y=f(x)在[0,6]上的最大值与最小值；

（2）当函数y=f(x)的图像在（0,6）上与x轴有唯一的公共点时，求实数a的取值范围。

已知函数f(x)=

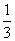x³-（2a+1）x²+3a（a+2）x+1，a∈R。
（1）当a=0时，求曲线y=f(x)在点（3，f(3)）处的切线方程；
（2）当a=-1时，求函数y=f(x)在[0，4]上的最大值和最小值；
（3）当函数y=f′(x)在（0，4）上有唯一的零点时，求实数a的取值范围．

求函数y=3x+(x＞0)的最值.