题目内容
在直角坐标系中,已知点P(x,y).O为坐标原点.
(1)若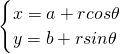 (其中a、b、r是常数,且r>0),求证:(x-a)2+(y-b)2=r2.
(其中a、b、r是常数,且r>0),求证:(x-a)2+(y-b)2=r2.
(2)若点A(2,4),M(2x-1,22y-1),N(4y,2x),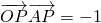 ,求u=
,求u=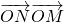 的取值范围.
的取值范围.
解:(1)由cos2θ+cos2θ=1 消去θ即得 (x-a)2+(y-b)2=r2.
(2)由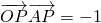 ,可得 x(x-2)+y(y-4)=-1,∴(x-1)2+(y-2)2=4.
,可得 x(x-2)+y(y-4)=-1,∴(x-1)2+(y-2)2=4.
令x=1+2cosθ,y=2+2sinθ,又u=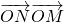 =2x-1•4y +22y-1•2x =2x+2y ,
=2x-1•4y +22y-1•2x =2x+2y ,
又x+2y=5+2cosθ+4sinθ=5+2 sin(θ+∅),cos∅=
sin(θ+∅),cos∅= ,sin∅=
,sin∅=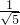 ,
,
∴ ,∴u的取值范围为
,∴u的取值范围为 .
.
分析:(1)由cos2θ+cos2θ=1 消去θ,即得 要证的等式.
(2)由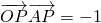 ,可得 (x-1)2+(y-2)2=4,又u=
,可得 (x-1)2+(y-2)2=4,又u=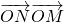 =2x+2y ,根据
=2x+2y ,根据
x+2y=5+2 sin(θ+∅),求出x+2y的范围,即可得到u的取值范围.
sin(θ+∅),求出x+2y的范围,即可得到u的取值范围.
点评:本题考查圆的参数方程,把参数方程化为普通方程的方法,两个向量的数量积,正弦函数的值域,
(2)由
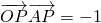 ,可得 x(x-2)+y(y-4)=-1,∴(x-1)2+(y-2)2=4.
,可得 x(x-2)+y(y-4)=-1,∴(x-1)2+(y-2)2=4.令x=1+2cosθ,y=2+2sinθ,又u=
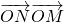 =2x-1•4y +22y-1•2x =2x+2y ,
=2x-1•4y +22y-1•2x =2x+2y ,又x+2y=5+2cosθ+4sinθ=5+2
 sin(θ+∅),cos∅=
sin(θ+∅),cos∅= ,sin∅=
,sin∅=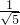 ,
,∴
 ,∴u的取值范围为
,∴u的取值范围为 .
.分析:(1)由cos2θ+cos2θ=1 消去θ,即得 要证的等式.
(2)由
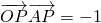 ,可得 (x-1)2+(y-2)2=4,又u=
,可得 (x-1)2+(y-2)2=4,又u=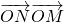 =2x+2y ,根据
=2x+2y ,根据x+2y=5+2
 sin(θ+∅),求出x+2y的范围,即可得到u的取值范围.
sin(θ+∅),求出x+2y的范围,即可得到u的取值范围.点评:本题考查圆的参数方程,把参数方程化为普通方程的方法,两个向量的数量积,正弦函数的值域,

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目
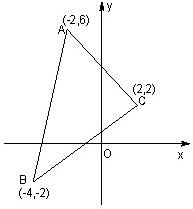 如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求:
如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求: 如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB: