题目内容

已知A(－，0)，B是圆F：(x－)2＋y2＝4(F为圆心)上一动点，线段AB的垂直平分线交BF于点P，则动点P的轨迹方程为　　　　　.

如图，连接PA.

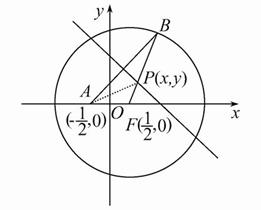
依题意可知|PA|＝|PB|，

∴|PA|＋|PF|＝|PB|＋|PF|＝|BF|＝2，

∴P点轨迹为以A(－，0)，F(，0)为焦点，长半轴长为1的椭圆.

其方程可设为＋＝1.

又∵c＝，a＝1，

∴b2＝a2－c2＝.

故P点的轨迹方程为x2＋y2＝1.

答案：x2＋y2＝1

练习册系列答案
相关题目
已知
a
=(1，0)，
b
=(1，1)，若向量λ
a
+
b
与向量
c
=(6，2)共线，则实数λ=
 
．
已知A(-
1
2
，0)，B是圆F：(x-
1
2
)2+y2=4(F为圆心）上一动点，线段AB的垂直平分线交BF于P，则动点P的轨迹方程为
 
．
已知
a
=(1，0)，
b
=(2，1)，若向量k
a
-
b
与
a
+3
b
平行，则实数k=
-
1
3
-
1
3
．
已知
a
=(2，0)，
b
=(1，2)，
求（1）
a
+3
b
；
（2）当k为何实数时，k
a
-
b
与
a
+3
b
平行，平行时它们是同向还是反向？
（2005•静安区一模）已知
a
=(1，0)，
b
=(2，1)，且向量k
a
-
b
与
a
+3
b
平行，则下列说法正确的是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网