Question

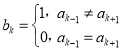【题目】已知有穷数列A：（且）.定义数列A的“伴生数列”B：，其中（），规定，.

（1）写出下列数列的“伴生数列”：

①1，2，3，4，5；

②1，，1，，1.

（2）已知数列B的“伴生数列”C：，，…，，…，，且满足（，2，…，n）.

（i）若数列B中存在相邻两项为1，求证：数列B中的每一项均为1；

（ⅱ）求数列C所有项的和.

Answer 1

【答案】（1）①1，1，1，1，1②1，0，0，0，1（2）（i）证明见解析（ⅱ）所有项的和或（n是3的倍数）

【解析】

（1）根据“伴生数列”的定义求解即可；

（2）（i）设存在，使得，讨论和，结合“伴生数列”的定义证明即可；

（ⅱ）利用反证法得出不可能存在，，再对数列的前三项，，的值进行讨论，当时，得出所有项的和；当，，时，得出与已知矛盾；当，，时，结合“伴生数列”的定义得出所有项的和，同理可以得出当，，及，，时，所有项的和.

解：（1）①1，1，1，1，1；

②1，0，0，0，1.

（2）（i）由题意，存在，使得.

若，即时，.

于是，.

所以，所以.即.

依次类推可得（，3，…，）.

所以（，2，…，n）.

若，由得.

于是.所以.

依次类推可得.

所以（，2，…，n）.

综上可知，数列B中的每一项均为1.

（ⅱ）首先证明不可能存在使得.

若存在使得，

则.

又得与已知矛盾.

所以不可能存在，.

由此及（ⅰ）得数列的前三项，，的可能情况如下：

当时，由（i）可得（，2，…，n）.

于是（，2，…，n）.

所以所有项的和.

当，，时，，

此时与已知矛盾.

当，，时，，，.

于是，.

故，，

于是，，，

于是，，，且，，.

依次类推且n恰是3的倍数满足题意.

所以所有项的和.

同理可得，，及，，时，

当且仅当n恰是3的倍数时，满足题意.

此时所有项的和.

综上，所有项的和或（n是3的倍数）.