题目内容
已知向量a=(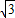 sinωx,cosωx),b=(cosωx,-cosωx),(ω>0),函数
sinωx,cosωx),b=(cosωx,-cosωx),(ω>0),函数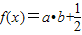 的图象的两相邻对称轴间的距离为
的图象的两相邻对称轴间的距离为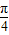 .
.(1)求ω值;
(2)若
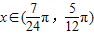 时,
时,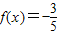 ,求cos4x的值;
,求cos4x的值;(3)若
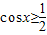 ,x∈(0,π),且f(x)=m有且仅有一个实根,求实数m的值.
,x∈(0,π),且f(x)=m有且仅有一个实根,求实数m的值.
【答案】分析:(1)先利用二倍角公式和两角和公式对函数解析式化简整理,然后利用两相邻对称轴间的距离求得函数的周期,进而根据周期公式求得ω.
(2)根据(1)中整理函数解析式,依据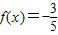 和同角三角函数的基本关系求得cos(4x-
和同角三角函数的基本关系求得cos(4x- )的值,进而根据
)的值,进而根据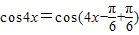 利用两角和公式求得答案.
利用两角和公式求得答案.
(3)根据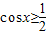 和余弦函数的单调性求得x的范围,令g(x)=m,则可作出,f(x)和g(x)的图象,利用数形结合的方法求得m的值.
和余弦函数的单调性求得x的范围,令g(x)=m,则可作出,f(x)和g(x)的图象,利用数形结合的方法求得m的值.
解答:解:由题意,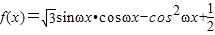
=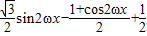
=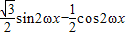 =
=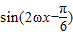 ,
,
(1)∵两相邻对称轴间的距离为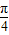 ,
,
∴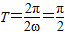 ,
,
∴ω=2.
(2)由(1)得,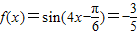 ,
,
∵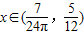 ,
,
∴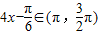 ,
,
∴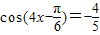 ,
,
∴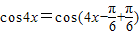 =
=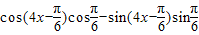
=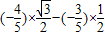 =
=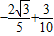 .
.
(3)∵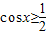 ,且余弦函数在(0,π)上是减函数,
,且余弦函数在(0,π)上是减函数,
∴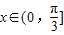 ,
,
令 =
=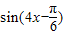 ,g(x)=m,在同一直角坐标系中作出两个函数的图象,
,g(x)=m,在同一直角坐标系中作出两个函数的图象,
可知m=1或m=- .
.
点评:本题主要考查了三角函数的周期性及其求法,两角和公式的化简求值,正弦函数和余弦函数的单调性.考查了三角函数基础知识的综合运用.
(2)根据(1)中整理函数解析式,依据
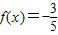 和同角三角函数的基本关系求得cos(4x-
和同角三角函数的基本关系求得cos(4x- )的值,进而根据
)的值,进而根据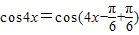 利用两角和公式求得答案.
利用两角和公式求得答案.(3)根据
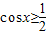 和余弦函数的单调性求得x的范围,令g(x)=m,则可作出,f(x)和g(x)的图象,利用数形结合的方法求得m的值.
和余弦函数的单调性求得x的范围,令g(x)=m,则可作出,f(x)和g(x)的图象,利用数形结合的方法求得m的值.解答:解:由题意,
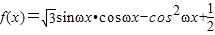
=
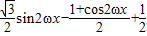
=
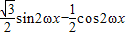 =
=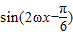 ,
,(1)∵两相邻对称轴间的距离为
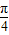 ,
,∴
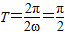 ,
,∴ω=2.
(2)由(1)得,
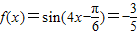 ,
,∵
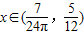 ,
,∴
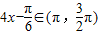 ,
,∴
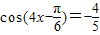 ,
,∴
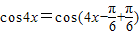 =
=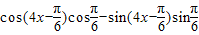
=
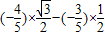 =
=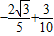 .
.(3)∵
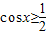 ,且余弦函数在(0,π)上是减函数,
,且余弦函数在(0,π)上是减函数,∴
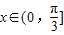 ,
,令
 =
=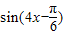 ,g(x)=m,在同一直角坐标系中作出两个函数的图象,
,g(x)=m,在同一直角坐标系中作出两个函数的图象,可知m=1或m=-
 .
.点评:本题主要考查了三角函数的周期性及其求法,两角和公式的化简求值,正弦函数和余弦函数的单调性.考查了三角函数基础知识的综合运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目