题目内容
设p：f（x）=lnx+2x2+mx+1在（0，+∞）内单调递增，q：m≥-5，则p是q的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
若f（x）=lnx+2x2+mx+1在（0，+∞）内单调递增，则f′（x）=
+4x+m≥0在（0，+∞）上恒成立
即m≥-（
+4x）在（0，+∞）上恒成立
∵-（
+4x）≤-2
=-4
∴m≥-4，∵{m|m≥-4}⊆{m|m≥-5}
∴p是q的充分不必要条件
故选A
| 1 |
| x |
即m≥-（
| 1 |
| x |
∵-（
| 1 |
| x |
|
∴m≥-4，∵{m|m≥-4}⊆{m|m≥-5}
∴p是q的充分不必要条件
故选A
练习册系列答案
相关题目
设P：f(x)=ln(2x)+
mx3-
x2+4x+1在[
，6]内单调递增，q：m≥
，则q是p的（ ）
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 6 |
| 5 |
| 9 |
| A、充分必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
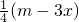在[2，4]上有两个不相等的实数根，求实数m的取值范围；（参考数据：e=2.71 828…）