题目内容
已知动点H到直线x-4=0的距离与到点(2,0)的距离之比为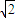 .
.(Ⅰ) 求动点H的轨迹E的方程;
(Ⅱ)是否存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A、B,且
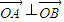 ?若存在,写出该圆的方程,若不存在说明理由.
?若存在,写出该圆的方程,若不存在说明理由.
【答案】分析:(Ⅰ)设动点H(x,y),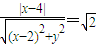 ,由此能求出动点H的轨迹E的方程.
,由此能求出动点H的轨迹E的方程.
(Ⅱ)假设存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1,y1),B(x2,y2),且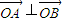 ,当圆的切线不垂直x轴时,设该圆的切线方程为y=kx+m,与x2+2y2=8联立方程得(1+2k2)x2+4kmx+2m2-8=0,再由根的判别式和韦达定理能够得到所求的圆.当切线的斜率不存在时,切线
,当圆的切线不垂直x轴时,设该圆的切线方程为y=kx+m,与x2+2y2=8联立方程得(1+2k2)x2+4kmx+2m2-8=0,再由根的判别式和韦达定理能够得到所求的圆.当切线的斜率不存在时,切线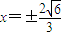 ,与椭圆x2+2y2=8的两个交点为
,与椭圆x2+2y2=8的两个交点为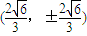 或
或 ,满足
,满足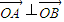 .由此知存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1,y1),B(x2,y2)且
.由此知存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1,y1),B(x2,y2)且 .
.
解答:解:(Ⅰ)设动点H(x,y)(1分)
∴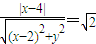 (3分)
(3分)
∴动点H的轨迹E的方程为x2+2y2=8,(4分)
(Ⅱ)假设存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1,y1),B(x2,y2)且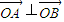 ,
,
①当圆的切线不垂直x轴时,设该圆的切线方程为y=kx+m,
与x2+2y2=8联立方程得(1+2k2)x2+4kmx+2m2-8=0,
∴△=8(8k2-m2+4)>0,
∴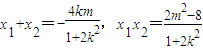 ,(5分)
,(5分)
∴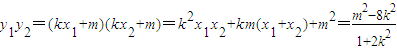 ,(6分)
,(6分)
∵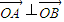 ,
,
∴x1x2+y1y2=0,
∴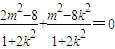 ,
,
∴3m2-8k2-8=0,
∴8k2=3m2-8,(7分)
∴对任意k,符合条件的m满足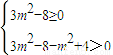 ,
,
∴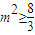 ,即
,即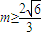 或
或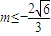 ,(8分)
,(8分)
∵直线y=kx+m为圆心在原点的圆的一条切线,
∴所以圆的半径为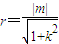 ,
,
∴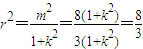 ,
,
∴所求的圆为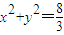 ,(9分)
,(9分)
此时该圆的切线y=kx+m都满足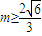 或
或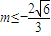 ,分
,分
∴所求的圆为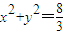 ,(10分)
,(10分)
②当切线的斜率不存在时,切线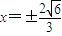 ,
,
与椭圆x2+2y2=8的两个交点为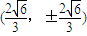 或
或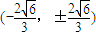 ,
,
满足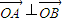 ,(11分)
,(11分)
综上,存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1,y1),B(x2,y2)且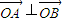 .
.
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,合理地进行等价转化,注意耐心地进行计算,避免不必要的错误.
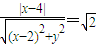 ,由此能求出动点H的轨迹E的方程.
,由此能求出动点H的轨迹E的方程.(Ⅱ)假设存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1,y1),B(x2,y2),且
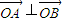 ,当圆的切线不垂直x轴时,设该圆的切线方程为y=kx+m,与x2+2y2=8联立方程得(1+2k2)x2+4kmx+2m2-8=0,再由根的判别式和韦达定理能够得到所求的圆.当切线的斜率不存在时,切线
,当圆的切线不垂直x轴时,设该圆的切线方程为y=kx+m,与x2+2y2=8联立方程得(1+2k2)x2+4kmx+2m2-8=0,再由根的判别式和韦达定理能够得到所求的圆.当切线的斜率不存在时,切线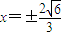 ,与椭圆x2+2y2=8的两个交点为
,与椭圆x2+2y2=8的两个交点为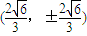 或
或 ,满足
,满足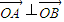 .由此知存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1,y1),B(x2,y2)且
.由此知存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1,y1),B(x2,y2)且 .
.解答:解:(Ⅰ)设动点H(x,y)(1分)
∴
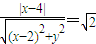 (3分)
(3分)∴动点H的轨迹E的方程为x2+2y2=8,(4分)
(Ⅱ)假设存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1,y1),B(x2,y2)且
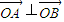 ,
,①当圆的切线不垂直x轴时,设该圆的切线方程为y=kx+m,
与x2+2y2=8联立方程得(1+2k2)x2+4kmx+2m2-8=0,
∴△=8(8k2-m2+4)>0,
∴
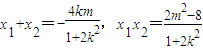 ,(5分)
,(5分)∴
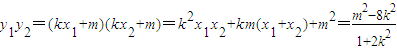 ,(6分)
,(6分)∵
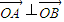 ,
,∴x1x2+y1y2=0,
∴
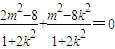 ,
,∴3m2-8k2-8=0,
∴8k2=3m2-8,(7分)
∴对任意k,符合条件的m满足
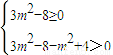 ,
,∴
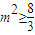 ,即
,即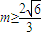 或
或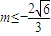 ,(8分)
,(8分)∵直线y=kx+m为圆心在原点的圆的一条切线,
∴所以圆的半径为
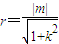 ,
,∴
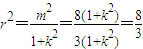 ,
,∴所求的圆为
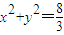 ,(9分)
,(9分)此时该圆的切线y=kx+m都满足
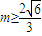 或
或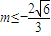 ,分
,分∴所求的圆为
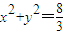 ,(10分)
,(10分)②当切线的斜率不存在时,切线
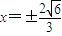 ,
,与椭圆x2+2y2=8的两个交点为
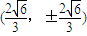 或
或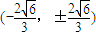 ,
,满足
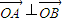 ,(11分)
,(11分)综上,存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1,y1),B(x2,y2)且
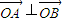 .
.点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,合理地进行等价转化,注意耐心地进行计算,避免不必要的错误.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 .
. ?若存在,写出该圆的方程,若不存在说明理由.
?若存在,写出该圆的方程,若不存在说明理由.