题目内容
已知动点H到直线x-4=0的距离与到点(2,0)的距离之比为| 2 |
(Ⅰ) 求动点H的轨迹E的方程;
(Ⅱ)是否存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A、B,且
| OA |
| OB |
分析:(Ⅰ)设动点H(x,y),
=
,由此能求出动点H的轨迹E的方程.
(Ⅱ)假设存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1,y1),B(x2,y2),且
⊥
,当圆的切线不垂直x轴时,设该圆的切线方程为y=kx+m,与x2+2y2=8联立方程得(1+2k2)x2+4kmx+2m2-8=0,再由根的判别式和韦达定理能够得到所求的圆.当切线的斜率不存在时,切线x=±
,与椭圆x2+2y2=8的两个交点为(
,±
)或(-
,±
),满足
⊥
.由此知存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1,y1),B(x2,y2)且
⊥
.
| |x-4| | ||
|
| 2 |
(Ⅱ)假设存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1,y1),B(x2,y2),且
| OA |
| OB |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
| OA |
| OB |
| OA |
| OB |
解答:解:(Ⅰ)设动点H(x,y)(1分)
∴
=
(3分)
∴动点H的轨迹E的方程为x2+2y2=8,(4分)
(Ⅱ)假设存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1,y1),B(x2,y2)且
⊥
,
①当圆的切线不垂直x轴时,设该圆的切线方程为y=kx+m,
与x2+2y2=8联立方程得(1+2k2)x2+4kmx+2m2-8=0,
∴△=8(8k2-m2+4)>0,
∴x1+x2=-
,x1x2=
,(5分)
∴y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=
,(6分)
∵
⊥
,
∴x1x2+y1y2=0,
∴
+
=0,
∴3m2-8k2-8=0,
∴8k2=3m2-8,(7分)
∴对任意k,符合条件的m满足
,
∴m2≥
,即m≥
或m≤-
,(8分)
∵直线y=kx+m为圆心在原点的圆的一条切线,
∴所以圆的半径为r=
,
∴r2=
=
=
,
∴所求的圆为x2+y2=
,(9分)
此时该圆的切线y=kx+m都满足m≥
或m≤-
,分
∴所求的圆为x2+y2=
,(10分)
②当切线的斜率不存在时,切线x=±
,
与椭圆x2+2y2=8的两个交点为(
,±
)或(-
,±
),
满足
⊥
,(11分)
综上,存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1,y1),B(x2,y2)且
⊥
.
∴
| |x-4| | ||
|
| 2 |
∴动点H的轨迹E的方程为x2+2y2=8,(4分)
(Ⅱ)假设存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1,y1),B(x2,y2)且
| OA |
| OB |
①当圆的切线不垂直x轴时,设该圆的切线方程为y=kx+m,
与x2+2y2=8联立方程得(1+2k2)x2+4kmx+2m2-8=0,
∴△=8(8k2-m2+4)>0,
∴x1+x2=-
| 4km |
| 1+2k2 |
| 2m2-8 |
| 1+2k2 |
∴y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=
| m2-8k2 |
| 1+2k2 |
∵
| OA |
| OB |
∴x1x2+y1y2=0,
∴
| 2m2-8 |
| 1+2k2 |
| m2-8k2 |
| 1+2k2 |
∴3m2-8k2-8=0,
∴8k2=3m2-8,(7分)
∴对任意k,符合条件的m满足
|
∴m2≥
| 8 |
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
∵直线y=kx+m为圆心在原点的圆的一条切线,
∴所以圆的半径为r=
| |m| | ||
|
∴r2=
| m2 |
| 1+k2 |
| 8(1+k2) |
| 3(1+k2) |
| 8 |
| 3 |
∴所求的圆为x2+y2=
| 8 |
| 3 |
此时该圆的切线y=kx+m都满足m≥
2
| ||
| 3 |
2
| ||
| 3 |
∴所求的圆为x2+y2=
| 8 |
| 3 |
②当切线的斜率不存在时,切线x=±
2
| ||
| 3 |
与椭圆x2+2y2=8的两个交点为(
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
满足
| OA |
| OB |
综上,存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1,y1),B(x2,y2)且
| OA |
| OB |
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,合理地进行等价转化,注意耐心地进行计算,避免不必要的错误.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
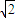 .
.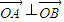 ?若存在,写出该圆的方程,若不存在说明理由.
?若存在,写出该圆的方程,若不存在说明理由. .
. ?若存在,写出该圆的方程,若不存在说明理由.
?若存在,写出该圆的方程,若不存在说明理由.