题目内容
【题目】在矩形ABCD中，AB=1，AD=2，动点P在以C为圆心且与BD相切的圆上，则
的最大值为（ ）
A. 
B. 
C. -2 D. 0
【答案】A
【解析】
如图：以A为原点，以AB，AD所在的直线为x，y轴建立如图所示的坐标系，先求出圆的标准方程，再设点P的坐标为（
cosθ+1，sinθ+2），
+1
，从而得到结果.
如图：以A为原点，以AB，AD所在的直线为x，y轴建立如图所示的坐标系，
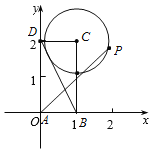
则A（0，0），B（1，0），D（0，2），C（1，2），
∵动点P在以点C为圆心且与BD相切的圆上，
设圆的半径为r，
∵BC=2，CD=1，
∴BD=
=
∴
BCCD=BDr，
∴r=
，
∴圆的方程为（x﹣1）2+（y﹣2）2=
，
设P
，则
∴+1
∴
的最大值为
故选：A
练习册系列答案
相关题目
【题目】某车间为了规定工时定额，需确定加工零件所花费的时间，为此做了4次试验，得到的数据如下：
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 4.5 |
若加工时间
与零件个数
之间有较好的相关关系．
（1）求加工时间与零件个数的线性回归方程
．
（2）试预报加工10个零件需要的时间．
附录：参考公式：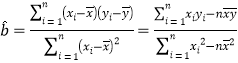
，
.
【题目】探究函数
的最小值，并确定取得最小值时x的值.列表如下：
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.002 | 4.04 | 4.3 | 5 | 4.8 | 7.57 | … |
请观察表中y值随x值变化的特点，完成以下的问题.
函数
在区间（0，2）上递减；
函数
在区间 上递增.
当
时， 
.
证明：函数
在区间（0，2）递减.
思考：函数
时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）
