Question

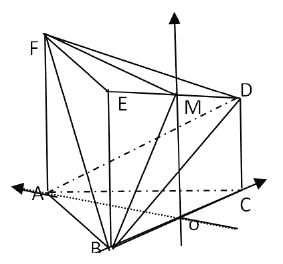
【题目】在如图所示的几何体中，正方形所在的平面与正三角形所在的平面互相垂直， ，且， 是的中点．

（1）求证： 平面；

（2）求面与面所成锐二面角的大小．

Answer 1

【答案】(1)见解析(2) 60°

【解析】试题分析：

（1）连接AE交BF于点N，连接MN，MN∥AD，由此能证明AD∥平面BFM．（2）推导出BE⊥AB，从而BE⊥平面ABC，取BC的中点O，连接OM，以O为坐标原点建立空间直角坐标系，利用向量法能求出二面角E-BM-F的余弦值．

解析：

（1）证明：

连接交于点，连接，

因为是正方形，所以是的中点，

又是的中点，所以，

因为平面平面，

所以平面；

（2）解法一：

因为是正方形，所以，因为平面平面，平面平面，所以平面，因为，所以取的中点．连接，则平面，因为是正三角形，所以，

所以以为坐标原点， 所在直线为轴建立如图所示的空间直角坐标系：设，

则，

，

设面的法向量为，

则，

令，则，

∴，

设面的法向量为，则

，

令，则， ∴，

，因为求面与面所成锐二面角， ∴平面与平面所成二面角的平面角为60°．

（2）解法二：

因为直线，所以面与面的交线与之平行，即，

分别取的中点，连，

因为，且，根据射影定理，所以，

所以，

所以，

所以为所求锐二面角的平面角，

设，则，

所以，

所以为正三角形，所以，

所以为所示锐二面角为60°．