题目内容
已知函数 ,
, ,
,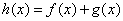 ,其中
,其中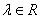 ,且
,且 .
.
(Ⅰ)当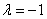 时,求函数
时,求函数 的最大值;
的最大值;
(Ⅱ)求函数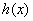 的单调区间;
的单调区间;
(III)设函数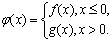 若对任意给定的非零实数
若对任意给定的非零实数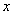 ,存在非零实数
,存在非零实数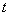 (
( ),使得
),使得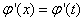 成立,求实数
成立,求实数 的取值范围.
的取值范围.
解:⑴当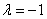 时,
时, ∴
∴
令 ,则
,则 , ∴
, ∴ 在
在 上单调递增,在
上单调递增,在 上单调递减
上单调递减
∴
⑵ ,
, ,(
,( )
)
∴当 时,
时, ,∴函数
,∴函数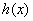 的增区间为
的增区间为 ,
,
当 时,
时, ,
,
当 时,
时, ,函数
,函数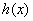 是减函数;当
是减函数;当 时,
时, ,函数
,函数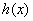 是增函数。
是增函数。
综上得,当 时,
时,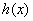 的增区间为
的增区间为 ;
;
当 时,
时,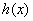 的增区间为
的增区间为 ,减区间为
,减区间为
⑶当 ,
, 在
在 上是减函数,此时
上是减函数,此时 的取值集合
的取值集合 ;
;
当 时,
时, ,
,
若 时,
时, 在
在 上是增函数,此时
上是增函数,此时 的取值集合
的取值集合 ;
;
若 时,
时, 在
在 上是减函数,此时
上是减函数,此时 的取值集合
的取值集合 。
。
对任意给定的非零实数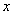 ,
,
①当 时,∵
时,∵ 在
在 上是减函数,则在
上是减函数,则在 上不存在实数
上不存在实数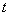 (
( ),使得
),使得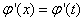 ,则
,则 ,要在
,要在 上存在非零实数
上存在非零实数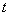 (
( ),使得
),使得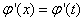 成立,必定有
成立,必定有 ,∴
,∴ ;
;
②当 时,
时, 在
在 时是单调函数,则
时是单调函数,则 ,要在
,要在 上存在非零实数
上存在非零实数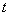 (
( ),使得
),使得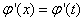 成立,必定有
成立,必定有 ,∴
,∴ 。
。
综上得,实数 的取值范围为
的取值范围为 。
。

练习册系列答案
相关题目
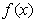 在R上是奇函数,且满足
在R上是奇函数,且满足 ,当
,当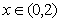 时,
时,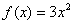 ,则
,则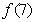 等于 。
等于 。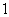 米的正方形,向
米的正方形,向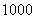 颗黄豆,数得落在正方形区域内
颗黄豆,数得落在正方形区域内
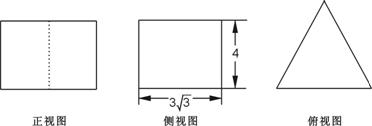
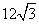 B.
B.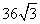 C.
C.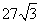 D.6
D.6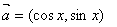 ,
,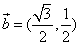 ,函数
,函数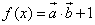 。
。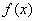 的值域和函数的单调递增区间;
的值域和函数的单调递增区间; 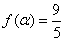 ,且
,且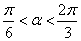 时,求
时,求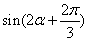 的值.
的值.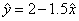 ,则变量
,则变量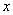 增加一个单位时( )
增加一个单位时( )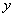 平均增加1.5个单位 B、
平均增加1.5个单位 B、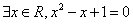 的否定是 ;
的否定是 ;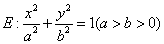 的右焦点为
的右焦点为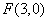 ,过点
,过点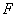 的直线交椭圆于
的直线交椭圆于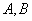 两点.若
两点.若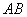 的中点坐标为
的中点坐标为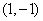 ,则
,则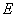 的方程为( )
的方程为( )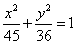 B.
B.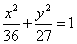 C.
C.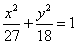 D.
D.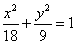
 ) C.(1,1,
) C.(1,1, ) D.(2,2,
) D.(2,2,