Question

【题目】某校高一举行了一次数学竞赛，为了了解本次竞赛学生的成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为）作为样本（样本容量）进行统计，按照、、、、的分组作出频率分布直方图，已知得分在、的频数分别为、.

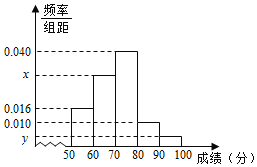
（1）求样本容量和频率分布直方图中的、的值；

（2）估计本次竞赛学生成绩的众数、中位数、平均数.

Answer 1

【答案】（1），，；（2）众数为，中位数为，平均数为.

【解析】

（1）由题意先根据得分在的频数求出样本容量，根据得分在的频数可计算出的值，再根据直方图中所有矩形面积之和为可求出的值；

（2）根据最高矩形底边中点值求出众数，将矩形底边的中点值乘以相应矩形的面积，再将所得结果相加可得平均数，设中位数为，根据中位数左边的矩形面积之和为列方程可求出的值，即为所求的中位数.

（1）由题意可知，样本容量为，，

；

（2）由频率分布直方图可知，本次竞赛学生成绩的众数为，

设中位数为，，则，

由题意可得，解得，

即本次竞赛学生成绩的中位数为.

由频率分布直方图可知，本次竞赛学生成绩的平均数为.