题目内容
设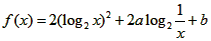 ,已知x=
,已知x=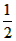 时,f(x)的最小值-8,
时,f(x)的最小值-8,
(1)求a和b的值;
(2)在(1)的条件下,求f(x)的解集A;
(3)设集合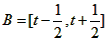 ,且A∩B=
,且A∩B=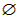 ,求实数t的取值范围。
,求实数t的取值范围。
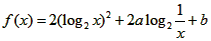 ,已知x=
,已知x=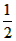 时,f(x)的最小值-8,
时,f(x)的最小值-8,(1)求a和b的值;
(2)在(1)的条件下,求f(x)的解集A;
(3)设集合
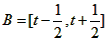 ,且A∩B=
,且A∩B=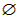 ,求实数t的取值范围。
,求实数t的取值范围。解:(1)令y=f(x)= ,t=log2x,
,t=log2x,
y=2t2-2at+b,由已知x= ,即t=-1时,f(x)由最小值-8
,即t=-1时,f(x)由最小值-8
的二次函数的对称轴为t= =-1,得a=-2
=-1,得a=-2
 =2×(-1)2-2×(-2)×(-1)+b=-8,得b=-6
=2×(-1)2-2×(-2)×(-1)+b=-8,得b=-6
即a与b的值分别为-2,-6
(2)即a与b的值分别为-2,-6
得
即 ,的log2x>1,或log2x<-3
,的log2x>1,或log2x<-3
即x>2,或0<x< ,得集合A=(0,
,得集合A=(0, )∪(2,+∞)
)∪(2,+∞)
(3)集合B= ,而A∩B=
,而A∩B= ,
,
得t+ ≤0,或
≤0,或 ,解得t≤
,解得t≤ ,或
,或 ≤t≤
≤t≤ ,
,
即实数t的取值范围为t≤ 或
或 ≤t≤
≤t≤
 ,t=log2x,
,t=log2x,y=2t2-2at+b,由已知x=
 ,即t=-1时,f(x)由最小值-8
,即t=-1时,f(x)由最小值-8的二次函数的对称轴为t=
 =-1,得a=-2
=-1,得a=-2 =2×(-1)2-2×(-2)×(-1)+b=-8,得b=-6
=2×(-1)2-2×(-2)×(-1)+b=-8,得b=-6即a与b的值分别为-2,-6
(2)即a与b的值分别为-2,-6
得

即
 ,的log2x>1,或log2x<-3
,的log2x>1,或log2x<-3即x>2,或0<x<
 ,得集合A=(0,
,得集合A=(0, )∪(2,+∞)
)∪(2,+∞)(3)集合B=
 ,而A∩B=
,而A∩B= ,
,得t+
 ≤0,或
≤0,或 ,解得t≤
,解得t≤ ,或
,或 ≤t≤
≤t≤ ,
,即实数t的取值范围为t≤
 或
或 ≤t≤
≤t≤

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 设函数f(x)是定义在区间(-∞,+∞)上以2为周期的函数,记Ik=(2k-1,2k+1](k∈Z).已知x∈I°时,f(x)=x2,如图.
设函数f(x)是定义在区间(-∞,+∞)上以2为周期的函数,记Ik=(2k-1,2k+1](k∈Z).已知x∈I°时,f(x)=x2,如图.