Question

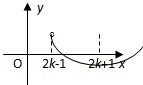
设函数f（x）是定义在区间（-∞，+∞）上以2为周期的函数，记I_k=（2k-1，2k+1]（k∈Z）．已知x∈I_°时，f（x）=x²，如图．
（1）求函数f（x）的解析式；
（2）对于k∈N^*，求集合M_k={a|使方程f（x）=ax在I_k上有两个不相等的实数根}．

Answer 1

分析：（1）利用函数的周期性求函数的表达式．（2）将方程f（x）=ax转化为二次函数，利用二次函数根的分布求a的取值集合．

解答：解：（1）因为f（x）是定义在区间（-∞，+∞）上以2为周期的函数，所以f（x）=f（x-2k），
当x∈I_k 时，（x-2k）∈I₀，所以f（x）=f（x-2k）=（x-2k）²．
所以函数f（x）的解析式为f（x）=f（x-2k）=（x-2k）²，x∈I_k．
（2）当k∈N^*，且x∈I_k 时，方程f（x）=ax化简为x²-（4k+a）x+k²=0，
设g（x）=x²-（4k+a）x+k²，使方程f（x）=ax在I_k上有两个不相等的实数根，
则

△=a(a+8k)＞0 2k-1＜ 4k+a 2 ≤2k+1 g(2k-1)=1-2ak+a＞0 g(2k+1)=1-2ak-a≥0

，即

a＞0??或a＜-8k -1＜a≤1 0＜a＜ 1 2k-1 0＜a≤ 1 2k+1

，解得0＜a≤

1

2k+1

，
所以M_k={a|0＜a≤

1

2k+1

}．

点评：本题主要考查函数周期性的应用，以及二次方程根的分布问题，考查学生的转化能力，综合性较强．