Question

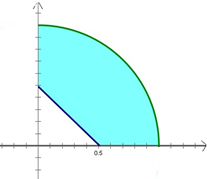在xoy平面中，将两坐标轴，线段x+y=

1

2

（x≥0，y≥0），和单位圆在第一象限的圆弧的所围成的几何图形（如图阴影部分）绕y轴旋转一周，求此图形在空间中所形成旋转体的全面积．

Answer 1

分析：几何体是图中阴影部分绕y轴旋转一周所得旋转体，是一个半球内挖去一个圆锥后剩余部分，求出圆锥的侧面积加上半球的表面积以及底面扇环的面积．

解答：解：如图所示，阴影部分绕y轴旋转所成旋转体是一个半球内挖去一个圆锥后剩余部分，
其的全面积是圆锥的侧面积加上半球的表面积以及底面扇环的面积，OA=1，OB=OC=

1

2

．
∴S_半球=

1

2

×4πr²=2π×1=4π，
S_圆锥=π×

1

2

×

2

2

=

2

4

π，
S_扇环=π×1-π×(

1

2

)2=

3

4

π，
∴S_全=4π+

2

4

π+

3

4

π．

点评：本题考查旋转体的表面积，组合体的表面积的求法，考查空间想象能力，是基础题．