Question

【题目】斜率为 的直线l与椭圆 + =1（a＞b＞0）交于不同的两点A、B．若点A、B在x轴上的射影恰好为椭圆的两个焦点．
（1）求椭圆的离心率；
（2）P是椭圆上的动点，若△PAB面积最大值是4 ，求该椭圆的方程．

Answer 1

【答案】
（1）解：由题意知：直线与椭圆两交点的横坐标为﹣c，c，纵坐标分别为﹣ ， ，

∴由 =

转化为：2b2=2（a2﹣c2）= ac

即2e2+ e﹣2=0，

解得e= ，e=﹣ （负根舍去），

∴椭圆的离心率为e= ；

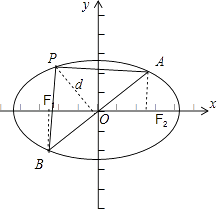
（2）解：∵P是椭圆上的动点，当△PAB的面积最大值是4 时，

有 |AB|h=4 ，

∵e= ，∴b=c，

∴a= c；

∴设椭圆的方程为 + =1，

则|AB|= c，

∴三角形PAB的高为h= ；

又直线为y= x，

即 x﹣2y=0；

则点P（ ccosθ，csinθ）到直线的距离表示为

d= = ≤ ，

令 = ，

解得c=2，

∴椭圆的方程为 + =1．

【解析】（1）画出图形，结合图形，得出直线与椭圆两交点坐标，根据两点间的斜率公式，求出离心率e；（2）由（1）知，设出椭圆的标准方程 + =1，求出|AB|的值，利用三角形的面积求出高h；再求点P到直线的最大距离d，由此求出c即可．
【考点精析】利用椭圆的标准方程对题目进行判断即可得到答案，需要熟知椭圆标准方程焦点在x轴：，焦点在y轴：．