题目内容
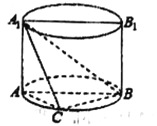
【题目】如图,已知面![]() 垂直于圆柱底面,
垂直于圆柱底面, ![]() 为底面直径,
为底面直径, ![]() 是底面圆周上异于
是底面圆周上异于![]() 的一点,
的一点, ![]() .求证:
.求证:
(1)平面![]() 平面
平面![]() ;
;
(2)求几何体![]() 的最大体积
的最大体积![]() .
.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)证明两个平面垂直,应用两面垂直的判定定理,在其中一个面内找一条直线与另一个面垂直。由![]() 为底面直径,
为底面直径, ![]() 是底面圆周上异于
是底面圆周上异于![]() 的一点,可得
的一点,可得![]() 。由面
。由面![]() 垂直于圆柱底面,可得
垂直于圆柱底面,可得![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() 。因为
。因为![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,再由直线与平面垂直的判定定理可得
,再由直线与平面垂直的判定定理可得![]() 平面
平面![]() .又因为
.又因为![]() 平面
平面![]() ,由面面垂直的判定定理可得平面
,由面面垂直的判定定理可得平面![]() 平面
平面![]() . (2)要求几何体
. (2)要求几何体![]() 的最大体积
的最大体积![]() ,应先把几何体的体积表示出来,转化为求函数的最值问题。该几何体是三棱锥,其体积为底面积与高的乘积三分之一,因为
,应先把几何体的体积表示出来,转化为求函数的最值问题。该几何体是三棱锥,其体积为底面积与高的乘积三分之一,因为![]() 平面
平面![]() ,所以
,所以![]() 是三棱锥
是三棱锥![]() 的高。因为
的高。因为![]() 为底面直径,且
为底面直径,且![]() ,故可设
,故可设![]() ,在
,在![]() 中,
中, ![]()
![]() 。所以三棱锥的体积为
。所以三棱锥的体积为
![]()
![]() ,因为
,因为![]() 为常数4,所以可由基本不等式求其最大值
为常数4,所以可由基本不等式求其最大值![]()
![]()
![]() .
.
试题解析:(1)证明:∵![]() 是底面圆周上异于
是底面圆周上异于![]() 的任意一点,且
的任意一点,且![]() 是圆柱底面圆的直径,∴
是圆柱底面圆的直径,∴![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]()
∵![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
∴![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)设![]() ,在
,在![]() 中,
中, ![]()
![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() 是三棱锥
是三棱锥![]() 的高
的高
因此,三棱锥的体积为
![]()
![]()
![]()
![]() .当且仅当
.当且仅当![]() ,即
,即![]() 时,三棱锥
时,三棱锥![]() 的体积取最大值。
的体积取最大值。
∴当![]() ,即
,即![]() 时,三棱锥
时,三棱锥![]() 的体积的最大值为
的体积的最大值为![]() .
.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
【题目】2017年6月深圳地铁总公司对深圳地铁1号线30个站的工作人员的服务态度进行了满意度调查,其中世界之窗、白石洲、高新园、深大、桃园、大新6个站的得分情况如下:
地铁站 | 世界之窗 | 白石州 | 高新园 | 深大 | 桃园 | 大新 |
满意度得分 | 70 | 76 | 72 | 70 | 72 | x |
已知6个站的平均得分为75分.
(1)求大新站的满意度得分x,及这6个站满意度得分的标准差;
(2)从表中前5个站中,随机地选2个站,求恰有1个站得分在区间(68,75)中的概率.