题目内容
已知P是椭圆
解:如图所示,P到l1的距离为d1,P到l2的距离为d2.

由第二定义知|PF1|=ed1,|PF2|=ed2.
又∵|PF1|2+|PF2|2=|F1F2|2,
∴e2d12+e2d22=(2c)2.
∴![]() (62+122)=4c2,a2=
(62+122)=4c2,a2=![]() =45.
=45.
又∵|PF1|+|PF2|=2a,
∴|PF1|2+2|PF1||PF2|+|PF2|2=4a2.
∴4c2+2e2d1d2=4a2.
∴4c2+![]() =4a2.
=4a2.
∴4c2+![]() c2=45×4.
c2=45×4.
∴![]() c2=45.
c2=45.
∴c2=![]() .∴c=
.∴c=![]() =5.
=5.
∴c2=25.
∴b2=a2-c2=20.
∴椭圆方程为![]() +
+![]() =1.
=1.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
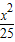 +
+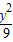 =1上的点,F1、F2分别是椭圆的左、右焦点,若
=1上的点,F1、F2分别是椭圆的左、右焦点,若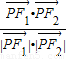 =
= ,则△F1PF2的面积为( )
,则△F1PF2的面积为( )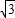
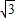
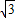
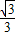
 +
+ =1上的一点,F1、F2是该椭圆的两个焦点,若△PF1F2的内切圆半径为
=1上的一点,F1、F2是该椭圆的两个焦点,若△PF1F2的内切圆半径为 ,则
,则 的值为( )
的值为( )

