题目内容
已知P为椭圆
=1(a＞b＞0)上一点，F1、F2为椭圆的焦点，若∠F1PF2＝θ.求证：S△F1PF2=b2tan
.
证明：由椭圆第一定义知，在△PF1F2中有|PF1|+|PF2|=2a，
由余弦定理得|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cosθ，
故2|PF1||PF2|cosθ=(|PF1|+|PF2|)2-2|PF1||PF2|-|F1F2|2，
即|PF1||PF2|(1+cosθ)=2b2，
∴S△F1PF2=|PF1||PF2|sinθ=·
sinθ=b2tan
.
注：（1）此结论称为焦点三角形面积公式，若将椭圆改为双曲线，其他条件不变，可求得S△F1PF2=b2cot
.（2）运用圆锥曲线统一定义可推导出焦半径公式.
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
+
=1上一点,P到一条准线的距离为P到相应焦点的距离之比为( )
B.
C.
D.
=1(a＞b＞0)上的一点,F1、F2是焦点,∠F1PF2=α.求证:
=b2tan
.
+
=1(a＞b＞0)上的点，P与两焦点F1、F2的连线互相垂直，且点P到两准线的距离分别为d1=6和d2=12，求椭圆方程.
（a＞b＞0）上一点，F1，F2是椭圆的左、右焦点，若使△PF1F2为直角三角形的点P有且只有4个，则椭圆离心率的取值范围是（ ）
）
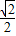，1）
）
，+∞）