题目内容
P正三角形ABC所在平面外一点,PA=PB=PC=
，且PA,PB,PC两两垂直，则P到面ABC的距离为（ ）
，且PA,PB,PC两两垂直，则P到面ABC的距离为（ ）| A． | B． | C．1 | D． |
C
试题分析： 先根据题意，由于P正三角形ABC所在平面外一点,PA=PB=PC=
，且PA,PB,PC两两垂直，故可知点P在底面的射影为底面的垂心，即为底面的重心，那么利用正三角形的性质可知，底面的边长为
，则底面的高线长为
，利用勾股定理可知P到面ABC的距离为1，选C.点评：解决该试题的关键是画出图形，过P作底面ABC 的垂线，垂足为O，连接CO并延长交AB于E，说明PO为所求
练习册系列答案
相关题目
上找一点M，在AD上找点N，使平面MED//平面BFN，说明理由；并求出
的值
中,
底面
,四边形
,
, 
,
,E为
中点.
的底面是直角三角形，
,点
在底面内的射影恰好是
的中点，且
.
平面
;
的余弦值为
,设
,求
的值.
＝
＝
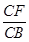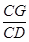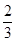，则（ ）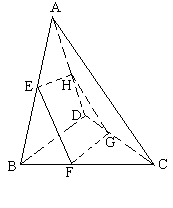
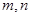是不同的直线，
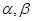是不同的平面，给出下列命题真命题是 
中，E是棱
的中点，则BE与平面
所成角的正弦值为
为三条不同的直线，
为一个平面，下列命题中不正确的是（ ）
，则
与
则
，
，
，
、
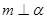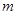是两条不同的直线，
、
是两个不同的平面.考查下列命题，其中正确的命题是（ ）
