题目内容
【题目】已知函数![]() ;
;![]() .
.
(1)判断![]() 在
在![]() 上的单调性,并说明理由;
上的单调性,并说明理由;
(2)求![]() 的极值;
的极值;
(3)当![]() 时,
时,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)极小值![]() .(3)
.(3)![]()
【解析】
(1)求导数,根据导函数符号确定单调性,(2)利用导数研究导函数单调性,根据单调性确定导函数符号变化规律,即得函数极值,(3)先根据特殊值得![]() ,再由(1)得
,再由(1)得![]() ,结合
,结合![]() 得
得![]() ,因此
,因此![]() ,最后利用(2)证明
,最后利用(2)证明![]() 满足条件.
满足条件.
解:(1)∵![]() ,
,
则![]() .
.
当![]() 时,
时,![]() ,
,![]() ,得
,得![]() ,
,
∴![]() 在
在![]() 上单调递减.
上单调递减.
(2)∵![]() ,
,
则![]() ,
,
令![]() ,则
,则![]() .
.
∴![]() 即
即![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,
,
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() 有极小值
有极小值![]() .
.
(3)令![]() ,
,
即![]() 对
对![]() 成立.
成立.
①![]() 时,
时,![]() 与
与![]() 矛盾,不成立.
矛盾,不成立.
②![]() 时,当
时,当![]() 时,
时,
令![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,∴
,∴![]() ,即
,即![]() .
.
由(2)知![]() .
.
当![]() 时,
时,![]() ,而
,而![]() ,等号不同时成立,
,等号不同时成立,
∴![]() .
.
③![]() 时,若
时,若![]() ,则
,则![]() ,
,
即![]() ,
,
由(1)知![]() ,
,
即![]() .
.
∴![]() ,
,
∴![]() 不成立.
不成立.
综上,![]() 的取值范围为
的取值范围为![]() .
.

【题目】近年来,随着互联网技术的快速发展,共享经济覆盖的范围迅速扩张,继共享单车、共享汽车之后,共享房屋以“民宿”、“农家乐”等形式开始在很多平台上线.某创业者计划在某景区附近租赁一套农房发展成特色“农家乐”,为了确定未来发展方向,此创业者对该景区附近六家“农家乐”跟踪调查了![]() 天.得到的统计数据如下表,
天.得到的统计数据如下表,![]() 为收费标准(单位:元/日),
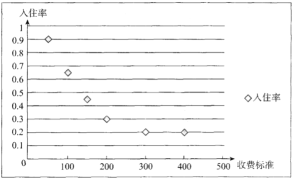
为收费标准(单位:元/日),![]() 为入住天数(单位:),以频率作为各自的“入住率”,收费标准
为入住天数(单位:),以频率作为各自的“入住率”,收费标准![]() 与“入住率”
与“入住率”![]() 的散点图如图
的散点图如图
x | 50 | 100 | 150 | 200 | 300 | 400 |
t | 90 | 65 | 45 | 30 | 20 | 20 |
(1)若从以上六家“农家乐”中随机抽取两家深入调查,记![]() 为“入住率”超过
为“入住率”超过![]() 的农家乐的个数,求
的农家乐的个数,求![]() 的概率分布列;
的概率分布列;
(2)令![]() ,由散点图判断
,由散点图判断![]() 与
与![]() 哪个更合适于此模型(给出判断即可,不必说明理由)?并根据你的判断结果求回归方程.(
哪个更合适于此模型(给出判断即可,不必说明理由)?并根据你的判断结果求回归方程.(![]() 结果保留一位小数)
结果保留一位小数)
(3)若一年按![]() 天计算,试估计收费标准为多少时,年销售额
天计算,试估计收费标准为多少时,年销售额![]() 最大?(年销售额
最大?(年销售额![]() 入住率
入住率![]() 收费标准
收费标准![]() )
)
参考数据: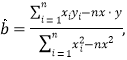
![]()
![]()
![]()