题目内容
2.求直线x-2y-6=0的斜率和在x轴、y轴上的截距.分析 先化为斜截式,再分别求出x=0,y=0,即可求出答案.
解答 解:x-2y-6=0等价于y=$\frac{1}{2}$x-3,
故直线x-2y-6=0的斜率为$\frac{1}{2}$,
当x=0时,y=-3,
当y=0时,x=6,
故在x轴、y轴上的截距为6,-3.
点评 本题考查了斜截式以及直线的截距,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
12.设a=${log_{\frac{1}{2}}}$3,b=${(\frac{1}{3})^{0.2}}$,c=${(\frac{1}{2})^{-\frac{1}{2}}}$,则( )
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<a<c |
17.△ABC的外接圆半径为R,C=60°,则$\frac{a+b}{R}$的取值范围是( )
| A. | [$\sqrt{3}$,2$\sqrt{3}$] | B. | [$\sqrt{3}$,2$\sqrt{3}$) | C. | ($\sqrt{3}$,2$\sqrt{3}$] | D. | ($\sqrt{3}$,2$\sqrt{3}$) |
14.有红、蓝颜色的旗帜各两面,在每种颜色的旗帜上分别标有号码1、2,从中任取两面,假设每面旗帜被取到的可能性相等,则取出的两面旗帜的颜色和号码均不相同的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
11.若a≥0,b≥0,且当$\left\{\begin{array}{l}{|x|≤1}\\{|y|≤1}\end{array}\right.$时,恒有2ax+by≤1,则点P(a+b,a-b)所形成的平面区域的面积是( )
| A. | $\frac{π}{2}$ | B. | 2π | C. | 1 | D. | $\frac{1}{2}$ |
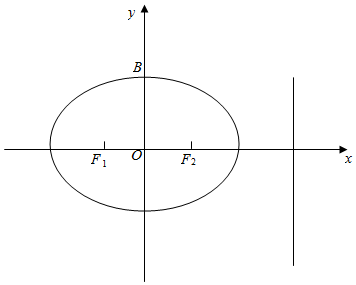 如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,点B(0,$\sqrt{3}$)是椭圆E的上顶点,F1,F2分别是椭圆E的左、右焦点.
如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,点B(0,$\sqrt{3}$)是椭圆E的上顶点,F1,F2分别是椭圆E的左、右焦点.