题目内容

正方体ABCD﹣A1B1C1D1的棱长为2，则B1C与平面A1BD间的距离为　　．

考点：

点、线、面间的距离计算．

专题：

空间位置关系与距离．

分析：

由题意，B1C与平面A1BD间的距离等于B1与平面A1BD间的距离，利用等体积，即可求得结论．

解答：

解：由题意，B1C与平面A1BD间的距离等于B1与平面A1BD间的距离，设为h，则

∵

∴

∴h=

故答案为：

点评：

本题考查线面距离，考查体积的计算，考查学生分析解决问题的能力，正确求体积是关键．

　

练习册系列答案
相关题目
两球O1和O2在棱长为1的正方体ABCD-A1B1C1D1的内部，且互相外切，若球O1与过点A的正方体的三个面相切，球O2与过点C1的正方体的三个面相切，则球O1和O2的表面积之和的最小值为（　　）
A、(6-3
3
)π
B、(8-4
3
)π
C、(6+3
3
)π
D、(8+4
3
)π
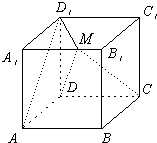如图，正方体ABCD-A1B1C1D1的棱长为6，动点M在棱A1B1上．
（1）求证：DM⊥AD1；
（2）当M为A1B1的中点时，求CM与平面DC1所成角的正弦值；
（3）当A1M=
34
A1B1时，求点C到平面D1DM的距离．
下面四个计算题中，结果正确的是
①②③
①②③
．（填序号）
①若|
a
|=2，|
b
|=3，且
a
与
b
的夹角为600，则|
a
-
b
|=
7
；
②棱长为2正方体ABCD-A1B1C1D1中，点A到平面BDD1B1的距离为d，则d=
2
；
③棱长都是1的平行六面体ABCD-A1B1C1D1中，∠BAD=∠BAA1=∠DAA1=600，则对角线的长AC1=
6
；
④在1200的二面角α-AB-β中AC?α，BD?β，AB⊥AC，AB⊥BD，AB=AC=BD=1，则点C与D的距离CD=
2
．
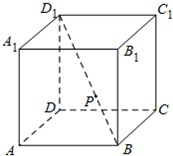（2013•北京）如图，在正方体ABCD-A1B1C1D1中，P为对角线BD1的三等分点，P到各顶点的距离的不同取值有（　　）
在正方体ABCD-A1B1C1D1中，异面直线BC1与AB1所成角的大小为（　　）
A、
π
2
B、
π
3
C、
π
4
D、
π
6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网