题目内容
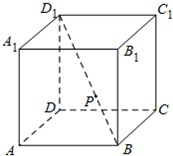（2013•北京）如图，在正方体ABCD-A1B1C1D1中，P为对角线BD1的三等分点，P到各顶点的距离的不同取值有（ ）分析：建立如图所示的空间直角坐标系，不妨设正方体的棱长|AB|=3，即可得到各顶点的坐标，利用两点间的距离公式即可得出．
解答：解：建立如图所示的空间直角坐标系，不妨设正方体的棱长|AB|=3，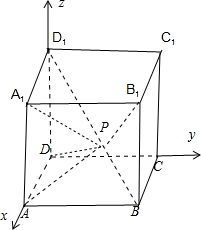
则A（3，0，0），B（3，3，0），C（0，3，0），D（0，0，0），A1（3，0，3），B1（3，3，3），C1（0，3，3），D1（0，0，3），
∴
=（-3，-3，3），设P（x，y，z），∵
=
=（-1，-1，1），∴
=
+(-1，-1，1)=（2，2，1）．
∴|PA|=|PC|=|PB1|=
=
，
|PD|=|PA1|=|PC1|=
=3，
|PB|=
，
|PD1|=
=2
．
故P到各顶点的距离的不同取值有
，3，
，2
共4个．
故选B．
则A（3，0，0），B（3，3，0），C（0，3，0），D（0，0，0），A1（3，0，3），B1（3，3，3），C1（0，3，3），D1（0，0，3），
∴
| BD1 |
| BP |
| 1 |
| 3 |
| BD1 |
| DP |
| DB |
∴|PA|=|PC|=|PB1|=
| 12+22+12 |
| 6 |
|PD|=|PA1|=|PC1|=
| 22+22+12 |
|PB|=
| 3 |
|PD1|=
| 22+22+22 |
| 3 |
故P到各顶点的距离的不同取值有
| 6 |
| 3 |
| 3 |
故选B．
点评：熟练掌握通过建立空间直角坐标系及两点间的距离公式是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
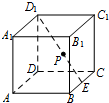（2013•北京）如图，在棱长为2的正方体ABCD-A1B1C1D1中，E为BC的中点，点P在线段D1E上，点P到直线CC1的距离的最小值为
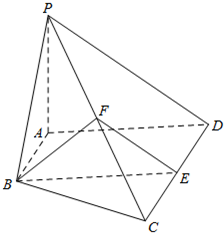（2013•北京）如图，在四棱锥P-ABCD中，AB∥CD，AB⊥AD，CD=2AB，平面PAD⊥底面ABCD，PA⊥AD．E和F分别是CD和PC的中点，求证：
（2013•北京）如图，在三棱柱ABC-A1B1C1中，AA1C1C是边长为4的正方形．平面ABC⊥平面AA1C1C，AB=3，BC=5．