题目内容
定义运算法则如下 ,
, ,
, ,
, ,则m+n=________.
,则m+n=________.
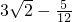
分析:根据新定义,由对数的运算性质和有理指数幂的化简求值分别求出m和n的值,然后作和.
解答:由
 ,知
,知 =
=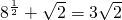 ,
,由
 ,知
,知 =
=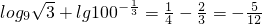 ,
,所以m+n=
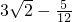 .
.故答案为
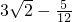 .
.点评:本题考查了新定义,考查了对数的运算性质和有理指数幂的化简求值,解答此题的关键是熟记有关性质,此题是基础题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
题目内容
 ,
, ,
, ,
, ,则m+n=________.
,则m+n=________.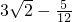
 ,知
,知 =
=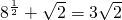 ,
, ,知
,知 =
=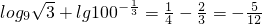 ,
,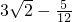 .
.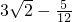 .
.
 活力课时同步练习册系列答案
活力课时同步练习册系列答案