题目内容
已知|
|=2，|
|=1，
•
=1．
（1）求|
+
|的值；
（2）若k
+
与
-3
垂直，求k的值．
| a |
| b |
| a |
| b |
（1）求|
| a |
| b |
（2）若k
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（1）利用数量积的运算性质即可得出；
（2）利用向量垂直与数量积的关系即可得出．
（2）利用向量垂直与数量积的关系即可得出．
解答：
解：（1）由|
+
|2=
2+
2+2
•
=4+1+2=7，
得|
+
|=
．
（2）由题意得(k
+
)•(
-3
)=0，
∴(k
+
)•(
-3
)=k
2-3
2+(1-3k)
•
=4k-3+1-3k=0，
解得k=2．
| a |
| b |
| a |
| b |
| a |
| b |
得|
| a |
| b |
| 7 |
（2）由题意得(k
| a |
| b |
| a |
| b |
∴(k
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
解得k=2．
点评：本题考查了数量积的运算性质、向量垂直与数量积的关系，属于基础题．
练习册系列答案
相关题目
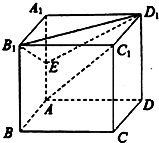如图，在正方体ABCD-A1B1C1D1中，
已知某几何体的直观图和三视图如图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形．点M是棱C1B1上的动点．